庫雷巴假設(Kurepas hypothesis)簡稱KH. 一個著名的組合論問題.設K為任意正規基數。
基本介紹
- 中文名:。
- 外文名:。
- 。:。
(T,<)為一棵高度為K的樹,若T的每個水平的基數均小於K,且T至少有K+條路徑,則稱<T,<)為一棵K庫雷巴樹,命題“存在K庫雷巴樹”稱為K庫雷巴假設,記為KH(動.所謂庫雷巴假設是指存在p庫雷巴樹,記為KH,因此KH即為KH<}c).相應地,。,庫雷巴樹稱為庫雷巴樹.從直觀上講,如果對樹中的每個水平的基數加以限制,則樹中所含的路徑的條數也受到了限制.但當K一。時,高度為。的完全二叉樹有2‘條路徑,由2},im+,因此。庫雷巴樹存在,即KH(c}).同理,當K為強不可達基數時,高度為K的完全二叉樹也是一棵K蘇斯林樹.人們自然會問,當}c>。且不是強不可達基數時,庫雷巴樹是否仍然成立?特別是當K一。1時,是否存在。:庫雷巴樹?斯特瓦特((Stewart, I.)利用力迫法證明庫雷巴假設相容於ZFC系統,但未公開發表其結果.1971年,他利用疊代力迫法證明了若ZFC十“強不可達基數存在”相容,則ZFC}-} KH也相容,從而證明了庫雷巴假設在ZFC系統中不可證.以色列學者索洛韋(Solovay, R. M.)於1972年利用延森(Jensen,R.)的結果證明了可構造性公理蘊含了庫雷巴假設,從而最終證明庫雷巴假設相容且獨立於ZFC系統.關於一般K庫雷巴樹的存在性則相當複雜.延森(Jessen,R.)與索洛韋證明若可構造性公理成立,則對每個正規基數}c ,“庫雷巴樹存在”等價於氣不是不可表達基數”.西爾維((Silver, J.)於1971年證明對某些“非特別”的正規基數K,在ZFC系統中可以證明K+庫雷巴樹存在.
KH (}c)有一種等價的純組合論表述形式:設K為正規基數,,0} C,9(}c),若}c}})}c+,且
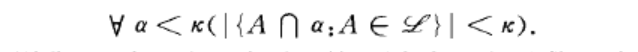
則稱.夕一為一個K庫雷巴簇.對任何正規基數K,存在K庫雷巴簇,等價於KH (}c).庫雷巴假設是庫雷巴(Kurepa , D.)於1935年以庫雷巴簇的形式提出的.目前關於庫雷巴樹的研究不僅仍然是無窮組合論研究的課題之一,而且在許多數學領域得到了廣泛的套用.
