極大元（maximal element）是偏序集中的一種特殊元素，指偏序集中沒有比它更大的可比較的元素。與此相關的概念還有，極小元：指偏序集中沒有與它可比較的更小的元素；最小元：指偏序集的子集中小於或等於一切元素的元素；最大元：指偏序集的子集中不小於一切的元素。
基本介紹
- 中文名：極大元
- 外文名：maximal element
- 涉及方面：離散數學
- 存在可能：多個
- 性質：偏序集中的一種特殊元素
- 相關：極小元、最小元、最大元
- 類型：偏序集中的特殊元素
簡介,相關概念,極小元,最小元,最大元,區分,
簡介
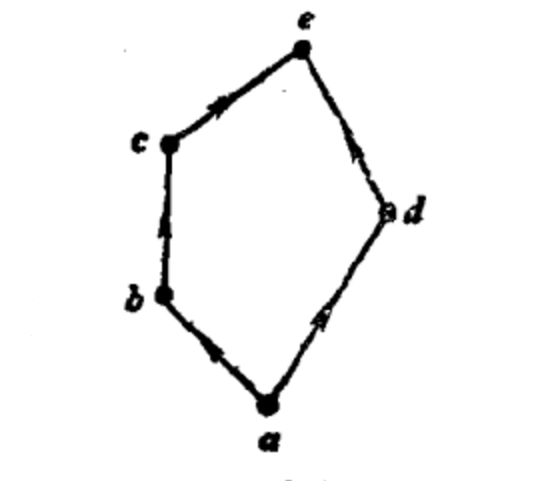
偏序集中的一種特殊元素，指偏序集中沒有比它更大的可比較的元素。設<A，R>是偏序集，
，若不存在
，使得 bRx 且x≠b，則b稱為<B，R>的極大元。對給定的<B，R>可以有一個或多個極大元，也可以沒有極大元。若a與b是<B，R>的兩個不同的極大元，則
且
。當B為有限集時，<B，R>一定有極大元。
相關概念
極小元
偏序集中的一種特殊元素，指偏序集中沒有與它可比較的更小的元素。設<A，R>是偏序集，，若不存在，使得 xRb 且 x≠b，則b稱為<B，R>的極小元。對給定的<B，R>可以有一個或多個極小元，也可以沒有極小元。若a與b是<B，R>的兩個不同的極小元，則且。當B為有限集時，<B，R>一定有極小元。
最小元
一種特殊元素，指偏序集的子集中小於或等於一切元素的元素。令<A，R>是偏序集，，如果對每一個都有bRx，則稱b是<B，R>的最小元。對給定的<B，R>不一定有最小元，若有最小元，則是惟一的。<A，R>的最小元稱為零元素，記為0。<B，R>的最小元是<B，R>的最大元；反之亦真。最小元是惟一的極小元。
最大元
一種特殊元素，指偏序集的子集中不小於一切元素的元素。令<A，R>是偏序集，，如果對每一個都有xRb，則稱b是<B，R>的最大元。對給定的<B，R>不一定有最大元，若有最大元，則是惟一的。<A，R>的最大元稱為單位元，記為1。<B，R>的最大元是<B，R>的最小元；反之亦真。最大元是惟一的極大元。
區分
設<A，R>偏序集，B含於A；
①若y∈B滿足任取x∈B，y≤x→x=y，則稱y為B的極大元；(箭頭表示“蘊含”)
②若y∈B滿足任取x∈B，x≤y，則稱y為B的最大元；
易得最大元必是極大元，但極大元不一定是最大元，應注意極大元和最大元的區別。 最大元是B中最大的元素，它與B中其它元素都可比；而極大元不一定與B中其它元素都可比，只要沒有比它大的元素，它就是極大元。對於有窮集合B，極大元一定存在，但最大元不一定存在。最大元如果存在一定是唯一的，但極大元可能有多個。
請注意極小元和最小元的區別。最小元是B中最小的元素，它與B中其它元素都可比；而極小元不一定與B中其它元素都可比，只要沒有比它小的元素，它就是極小元。對於有窮集合B極小元一定存在，但最小元不一定存在。最小元如果存在一定是唯一的，但極小元可能有多個。
