蓋爾曼矩陣

蓋爾曼矩陣（Gell-Mann matrices）是八個線性獨立且無跡的埃爾米特矩陣，是SU(3)群的李代數的一種基表示，以物理學家默里·蓋爾曼命名。蓋爾曼矩陣是為了分析強相互作用的味對稱性而提出的（u，d，s夸克之間的SU(3)對稱性），廣泛套用於強子分類。而之後物理學家們在分析其他SU(3)對稱性時都會選取這種表示（比如色的SU(3)對稱性）。

基本介紹

• 中文名：蓋爾曼矩陣
• 外文名：Gell-Mann matrices

定義

（i=1到8）表示如下：

物理學中常用另一種形式的蓋爾曼矩陣 。

性質

蓋爾曼矩陣是無跡的埃爾米特矩陣（故可以通過指數運算生成么正矩陣），並滿足跡正交關係。這些性質是由蓋爾曼選定的，因為這樣自然地把SU(2)的泡利矩陣推廣到SU(3)，構成了蓋爾曼夸克模型的基礎。蓋爾曼的推廣還可進一步擴展到一般的SU(n)上。

跡正交性

其中 是克羅內克δ。

有三個獨立的SU(2)子代數： ， 與 。其中 與 都是 的線性組合。這些子代數的任意么正相似變換仍然是SU(2)子代數。

這樣的好處是以 作坐標軸畫權圖時，兩坐標軸是垂直的。在這樣定義下基礎表示與其共軛表示的權圖是關於 軸對稱的正三角形，見下圖1

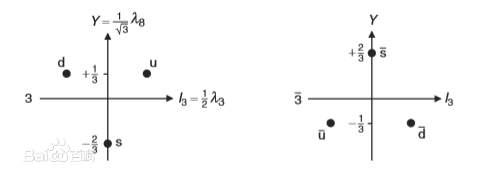
圖1

對易關係

蓋爾曼矩陣滿足對易關係

結構常數 關於三個指標是完全反對稱的，類似於列維-奇維塔符號 。它們的非零分量為

完備性關係

八個蓋爾曼矩陣與單位矩陣一起構成了完備的跡正交集，能生成所有的3×3矩陣。因此可以直接找到兩個完備性關係，就像泡利矩陣所滿足的那樣。第 個蓋爾曼矩陣的第 行第 列的元素記做 ，並記

則以下恆等式成立

表示論

SU(3)中的任何元素都可以寫成 的形式，其中 是八個實數，並使用愛因斯坦求和約定。

蓋爾曼矩陣的平方和給出了二次卡西米爾運算元

套用

蓋爾曼矩陣在強子分類中有重大意義。 為u，d夸克SU(2)同位旋空間的第三分量，可以表達為：

類似於超荷，物理意義為：

其中n為對應夸克數，Q為電荷。

由 與 表示的直積化直和，生成伴隨表示8，就可以給出對輕夸克組成的介子的8重態分類，具體見下圖2

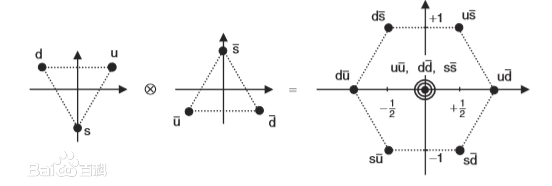
圖2

在量子色動力學中，蓋爾曼矩陣可用來研究膠子場的“色”旋轉。規範色旋轉可表示為