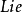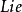和一個群的任何運算元都可對易的運算元,稱為這個群的卡西米爾運算元(Caslmtr operator)。卡西米爾運算元的個數等於群的秩,它們一起構成一個完全組。卡西米爾運算元的重要性在於,這組運算元的本徵值可用來標記群的不可約表示,即它們的每一組本徵值都代表了一個不可約表示。例如,轉動群是秩為1的李群,有一個卡西米爾運算元,即角動量的平方,因而轉動群的不可約表示就是用角動量的本徵值來標記的。
基本介紹
- 中文名:卡西米爾運算元
- 外文名:Caslmtr operator
- 定義:和一個群的任何運算元都可對易
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:李群
概念,基本原理,
概念
和一個群的任何運算元都可對易的運算元,稱為這個群的卡西米爾運算元(Caslmtroperator)。卡西米爾運算元的個數等於群的秩,它們一起構成一個完全組。卡西米爾運算元的重要性在於,這組運算元的本徵值可用來標記群的不可約表示,即它們的每一組本徵值都代表了一個不可約表示。例如,轉動群是秩為1的李群,有一個卡西米爾運算元,即角動量的平方,因而轉動群的不可約表示就是用角動量的本徵值來標記的。
基本原理
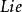
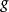
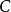

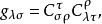
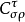
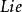
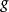
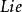
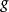
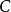

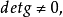
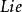
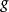
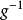
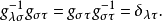
一般把逆張量的矩陣元記為 ,即
,即





定義運算元 為
為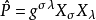 為半單
為半單 代數
代數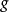 的卡西米爾運算元,
的卡西米爾運算元,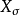 ,
,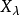 為半單
為半單 代數的基矢。
代數的基矢。

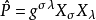

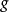
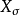
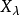

卡西米爾運算元具有一個重要的性質:半單 代數
代數 的卡西米爾運算元
的卡西米爾運算元 與
與 代數
代數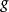 的所有元素都是交換的。
的所有元素都是交換的。




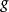
由於卡西米爾( )不變運算元與
)不變運算元與 代數的所有元素都是交換的,因而它們在半單
代數的所有元素都是交換的,因而它們在半單 代數和半單
代數和半單 群的表示理論研究中是十分有用的,可用它們的本徵值標記不可約表示的基矢。
群的表示理論研究中是十分有用的,可用它們的本徵值標記不可約表示的基矢。




由於度規張量非退化是半單 代數的充要條件,因而非半單
代數的充要條件,因而非半單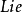 代數度規張量一定是退化的,不存在逆。這樣便不能定義卡西米爾(
代數度規張量一定是退化的,不存在逆。這樣便不能定義卡西米爾( )運算元。不過對於非半單
)運算元。不過對於非半單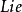 代數也可用其它方法定義與代數的所有元素都交換的運算元,一般稱為不變運算元。
代數也可用其它方法定義與代數的所有元素都交換的運算元,一般稱為不變運算元。