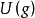基本介紹
- 中文名:卡西米爾不變數
- 外文名:Casimir element
- 別稱:卡西米爾元素
- 學科:數理科學
定義,二次卡西米爾元素,卡西米爾不變的線性表示和光滑的行動,屬性,獨特性,與G的拉普拉斯運算元,特徵值,
定義
卡西米爾不變數最簡單的定義是二次不變數。但是,也可能有卡西米爾不變數高階,這對應於高階齊次對稱多項式,下面給出了它們的定義。
二次卡西米爾元素

假設 表示
表示 的任意基礎形式,
的任意基礎形式, 表示
表示 關於
關於 的雙重基礎形式。對卡西米爾不變數
的雙重基礎形式。對卡西米爾不變數 的普遍包絡代數由下式給出:
的普遍包絡代數由下式給出:







卡西米爾不變的線性表示和光滑的行動
假定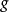 在向量空間
在向量空間 中表示為
中表示為 (可能是無限維的),卡西米爾不變數
(可能是無限維的),卡西米爾不變數 的定義是
的定義是 ,由V上的線性運算元得出下屬公式:
,由V上的線性運算元得出下屬公式:





屬性
獨特性
對於一個簡單的lie代數,每一個不變的雙線性形式是Killing形式的倍數,相應的Casimir元素被唯一地定義為一個常數。 對於一般半單李代數,不變雙線性形式的空間對於每個簡單分量都有一個基向量,因此對於相應的卡西米爾運算元的空間也是如此。
與G的拉普拉斯運算元
如果 為帶有lie代數的李群,那么在
為帶有lie代數的李群,那么在 上選擇一個不變的雙線性形式,
上選擇一個不變的雙線性形式, 對應於
對應於 上的一個雙不變黎曼度量。然後G上的左不變微分運算元在通用包絡代數的識別下,g的雙線性形式的卡西米爾不變數映射為G的拉普拉斯運算元。
上的一個雙不變黎曼度量。然後G上的左不變微分運算元在通用包絡代數的識別下,g的雙線性形式的卡西米爾不變數映射為G的拉普拉斯運算元。




特徵值
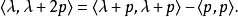
此外,如果 ,那么上述常數是非零。然後
,那么上述常數是非零。然後 且
且 ,這表明
,這表明 。這個觀察的證據起著重要的作用韋爾定理的完整還原性。
。這個觀察的證據起著重要的作用韋爾定理的完整還原性。