基本介紹
- 中文名:結構常數
- 外文名:structural constant
- 所屬學科:數學
- 相關概念:李代數、李群、同構等
基本介紹,交換子表,無窮小群作用,
基本介紹
若g是一個有限維李代數,則根據定理1,g是某個李群G的李代數。如果構想 是g的一組基,那么就存在一組常數
是g的一組基,那么就存在一組常數 使得
使得




(1)反對稱性:

(2)Jacobi恆等式:

由於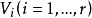 構成一組基,如果我們知道
構成一組基,如果我們知道 ,利用式(1)和李括弧的雙線性即可重新構造出李代數g來。因此稱滿足條件即式(2)和式(3)的常數組
,利用式(1)和李括弧的雙線性即可重新構造出李代數g來。因此稱滿足條件即式(2)和式(3)的常數組 為李代數g的結構常數。反之,不難證明,任意一組滿足式(2)和式(3)的常數
為李代數g的結構常數。反之,不難證明,任意一組滿足式(2)和式(3)的常數 都是某個李代數的結構常數。
都是某個李代數的結構常數。
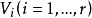



如果選取g的另一組基 為
為







因此,兩組結構常數確定同一個李代數的充分必要條件是:存在矩陣 ,使它們滿足式(5)。於是由定理1可見,在連通李群的李代數和滿足式(2)和式(3)的結構常數的等價類之間存在一一對應。所以,可以通過研究代數方程式(2)和式(3)來研究有限維李代數的性質,當然這並不能代替整個李群理論。
,使它們滿足式(5)。於是由定理1可見,在連通李群的李代數和滿足式(2)和式(3)的結構常數的等價類之間存在一一對應。所以,可以通過研究代數方程式(2)和式(3)來研究有限維李代數的性質,當然這並不能代替整個李群理論。

交換子表
展示一個李代數的結構,最方便的方法是用交換子表。如果g是一個r 維李代數, 是它們的一組基,那么g的交換子表就是一個
是它們的一組基,那么g的交換子表就是一個 表格,第(i,j)個元素就表示李括弧
表格,第(i,j)個元素就表示李括弧 。由於李括弧是反對稱的,交換子表也是反對稱的,特別是對角線上的元素為0。有了交換子表,結構常數就可以很方便地從交換子表中讀出,即
。由於李括弧是反對稱的,交換子表也是反對稱的,特別是對角線上的元素為0。有了交換子表,結構常數就可以很方便地從交換子表中讀出,即 就是交換子表中第(i,j)個元素里
就是交換子表中第(i,j)個元素里 的係數。
的係數。





以特殊線性群 的李代數
的李代數 為例說明交換子表的表示法。此時g由跡為零的2×2矩陣全體組成,取一組基為
為例說明交換子表的表示法。此時g由跡為零的2×2矩陣全體組成,取一組基為



A1 | A2 | A3 | |
A1 | 0 | A1 | -A2 |
A2 | -A1 | 0 | A3 |
A3 | 2A2 | -A3 | 0 |
例如,從表中可知 等。結構常數是
等。結構常數是 ,其他
,其他 全為零。
全為零。



無窮小群作用
下面簡要地介紹無窮小群作用。
設G是作用在流形M上的局部變換群,即

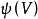
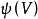







反之給定M上一個有限維向量場李代數,總存在一個局部變換群,其無窮小作用由已知李代數生成。因此有下面的定理。
定理2 設 是流形M上的滿足如下關係的向量場:
是流形M上的滿足如下關係的向量場:


式中, 是常數。那么存在一個李群G,其李代數以
是常數。那么存在一個李群G,其李代數以 為相對於某組基
為相對於某組基 的結構常數,並且G在M上的局部群作用使得曲
的結構常數,並且G在M上的局部群作用使得曲 由式(6)定義。
由式(6)定義。




通常,忽略對映射 的明顯依賴,而把李代數g和它的像
的明顯依賴,而把李代數g和它的像 視為等同。這樣,通過下面的公式從群變換可以重新得到g,即
視為等同。這樣,通過下面的公式從群變換可以重新得到g,即