菲涅耳積分(Fresnel integral)由積分定義的一類特殊函式.定義為
這類積分最初出現在光的衍射理論中，近年來在其他方面，例如高速公路迴旋設計中，也有套用.
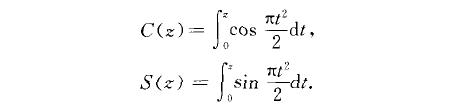
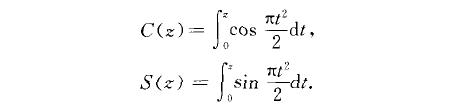
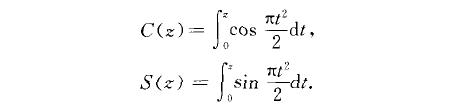
菲涅耳積分(Fresnel integral)由積分定義的一類特殊函式.定義為 這類積分最初出現在光的衍射理論中,近年來在其他方面,例如高速公路迴旋設計中,也有套用. ...
菲涅爾函式(Fresnel function)又稱菲涅爾積分(Fresnel integral)。...... 菲涅爾函式圖像 菲涅爾函式 [1] (Fresnel function)又稱菲涅爾積分(Fresnel integral)。...
在光學裡,菲涅耳數(Fresnel number)是一個時常出現於衍射理論的無量綱量。菲涅耳數是因法國物理學者奧古斯丁·菲涅耳而命名。...
菲涅耳公式(或菲涅耳方程),由奧古斯丁·讓·菲涅耳導出。用來描述光在不同折射率的介質之間的行為。由公式推導出的光的反射稱之為“菲涅爾反射”。菲涅爾公式是光學...
在光學裡,菲涅耳衍射(Fresnel diffraction)指的是光波在近場區域的衍射。菲涅耳衍射積分式可以用來計算光波在近場區域的傳播,因法國物理學者奧古斯丁·菲涅耳而命名,是...
基爾霍夫積分定理(Kirchhoff integral theorem)是因德國物理學者古斯塔夫·基爾霍夫而命名。這定理廣泛地套用於光學領域。對於很多案例,這定理的方程可以近似成一種更...
Astola找到了一個可被運用在離散傅立葉轉換的一般化菲涅爾轉換,並且得出有偶數次的離散傅立葉轉換有兩個一般化的菲涅爾轉換函式、奇數次的離散傅立葉轉換則只有一...
菲涅耳衍射(Fresnel diffraction)指的是光波在近場區域的衍射。在光學研究中,菲涅耳衍射積分式可以用來計算光波在近場區域的傳播。...
惠更斯-菲涅耳原理(英語:Huygens–Fresnel principle)是研究波傳播問題的一種分析方法,因荷蘭物理學者克里斯蒂安·惠更斯和法國物理學者奧古斯丁·菲涅耳而命名。這個原理...
特殊函式是指一些具有特定性質的函式,一般有約定俗成的名稱和記號,例如伽瑪函式、貝塞爾函式、菲涅耳積分等。它們在數學分析、泛函分析、物理研究、工程套用中有著舉足...
在光學裡,菲涅耳-基爾霍夫衍射公式(Fresnel-Kirchoff's diffraction formula)可以套用於光波傳播的理論分析模型或數值分析模型。[1][2]從菲涅耳-基爾霍夫衍射公式,...
觀測時,會看到菲涅耳衍射所產生的圓孔成像,大小與形狀會與原來的圓孔不一樣,即是說邊緣多少會有一些鋸齒在,但是夫琅和費衍射的成像則只有大小的改變,這是因為遠...
▪ 誤差函式 ▪ 菲涅耳積分 帕德逼近簡介 編輯 帕德是法國數學家亨利·帕德發明的有理多項式近似法。帕德近似往往比截斷的泰勒級數準確,而且當泰勒級數不收斂時,...
觀測時,會看到菲涅耳衍射所產生的圓孔成像,大小與形狀會與原來的圓孔不一樣,即是說邊緣多少會有一些鋸齒在,但是夫琅禾費衍射的成像則只有大小的改變,這是因為遠...
在衍射理論方面,對菲涅耳與夫琅和費衍射作了較詳細的討論,並對近年來新出現的無衍射光束作了介紹.本書對晶體光學的理論以及電光、磁光和聲光效應作了較為深入的...
刀口效應(Knife-edge effect)即電磁波傳播在遇到障礙物時,與障礙物邊緣相遇部分的電磁波傳播方向發生改變而進入障礙物的蔭影區域的這種現象。 可用惠更斯-菲涅耳原理...
這個初看起來似乎是荒謬的結論,是泊松研究菲涅耳論文時把它當作謬誤提出來的,但卻成了支持波動說的強有力的證據。後來人們為了紀念這一極具戲劇性事實,就把衍射...
5 10 2菲涅耳波帶法()5 10 3圓孔衍射圖樣()5 10 4圓屏的菲涅耳衍射()5 10 5菲涅耳波帶片()*5 11直邊的菲涅耳衍射()5 11 1菲涅耳積分及其圖解()5 ...