線性表示是一種重要的表達形式,指線性空間中的一個元素可通過另一組元素的線性運算來表示。零向量可由任一組向量線性表示。
基本介紹
- 中文名:線性表示
- 外文名:linear representation
- 性質:線性
- 舉例:零向量可由任一組向量線性表示。
- 領域:線性代數
- 學科:數學
定義

舉例
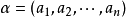
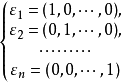
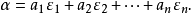
相關概念
等價向量組




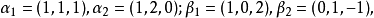
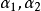

線性相關
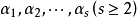
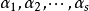
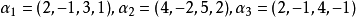
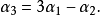
線性表示是一種重要的表達形式,指線性空間中的一個元素可通過另一組元素的線性運算來表示。零向量可由任一組向量線性表示。

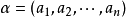
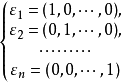
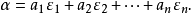

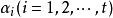



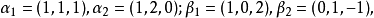

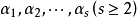
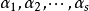
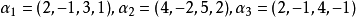
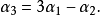
線性表示是一種重要的表達形式,指線性空間中的一個元素可通過另一組元素的線性運算來表示。零向量可由任一組向量線性表示。...
線性特性是卷積運算的性質之一,即設a,b為任意常數,則對於函式f(z,y),h(x,y)和g(x,y),{af(x,Y)+bh(z,y)}*g(z,y)=-af(x,y)*g(x,y)+bh...
兩個變數之間存在一次方函式關係,就稱它們之間存在線性關係。正比例關係是線性關係中的特例,反比例關係不是線性關係。更通俗一點講,如果把這兩個變數分別作為點的...
在數學裡,線性函式是指那些線性的函式,但也常用作一次函式的別稱,儘管一次函式不一定是線性的。線型函式是一個比較恰當的同義詞。...
在線性代數裡,矢量空間的一組元素中,若沒有矢量可用有限個其他矢量的線性組合所表示,則稱為線性無關或線性獨立(linearly independent),反之稱為線性相關(linearly ...
在V 上取一組基,把線性變換 ρ(g) 在此基下的矩陣記作 T(g),則 g→ T(g) 是 G 到一般線性群 GL(n,K) 內的同態,它稱為 G 的矩陣表示。...
單項表示(monomial representation)一類特殊的線性表示.一個n階方陣,若它的每行及每列至多只有一個元素不為零,則稱這個方陣為單項矩陣.設ρ是群G的一個線性表示...
線性特性是卷積運算的性質之一,即設a,b為任意常數,則對於函式f(z,y),h(x,y)和g(x,y),{af(x,Y)+bh(z,y)}*g(z,y)=-af(x,y)*g(x,y)+bh...
線性回歸是利用數理統計中回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法,運用十分廣泛。其表達形式為y = w'x+e,e為誤差服從均值為0...
線性組合是線性代數的基本概念之一,設α₁,α₂,…,αₑ(e≥1)是域P上線性空間V中的有限個向量,若V中向量α可以表示為α=k₁α₁+k₂α₂+...
等價表示(equivalent representations)數學結構相同的線性表示.設Pm P:是群G的兩個線性表示,表示空間分別為W ,VZ.若存在V,到Y:的同構f}使得對每個gEG有Pz } g...
線性回歸方程是利用數理統計中的回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法之一。線性回歸也是回歸分析中第一種經過嚴格研究並在實際...
