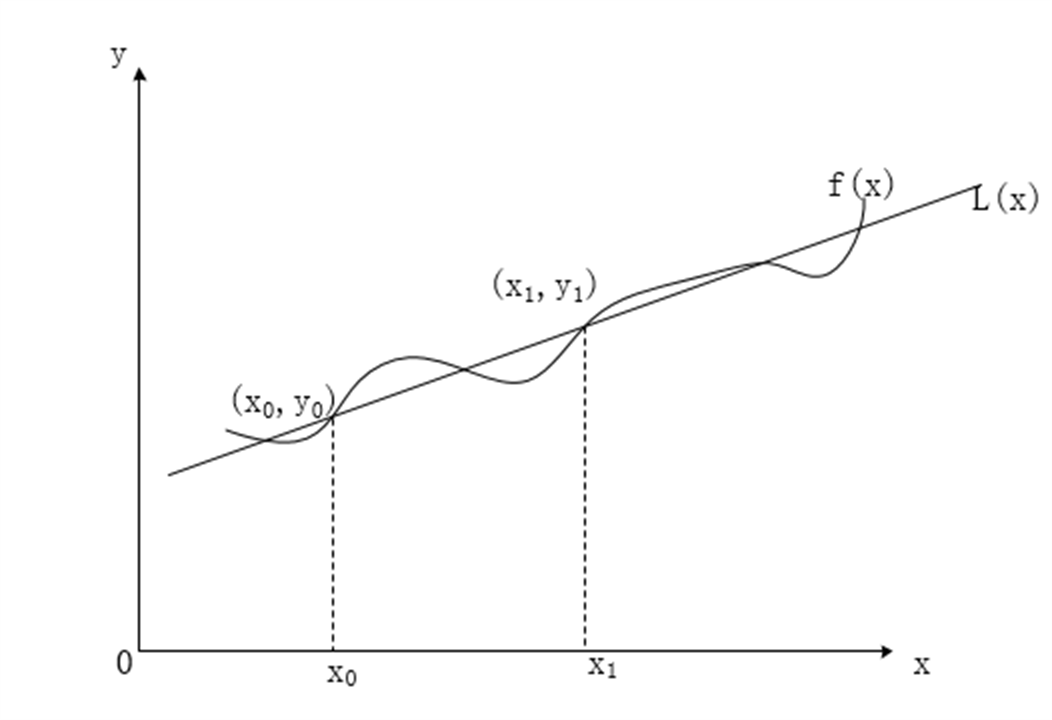
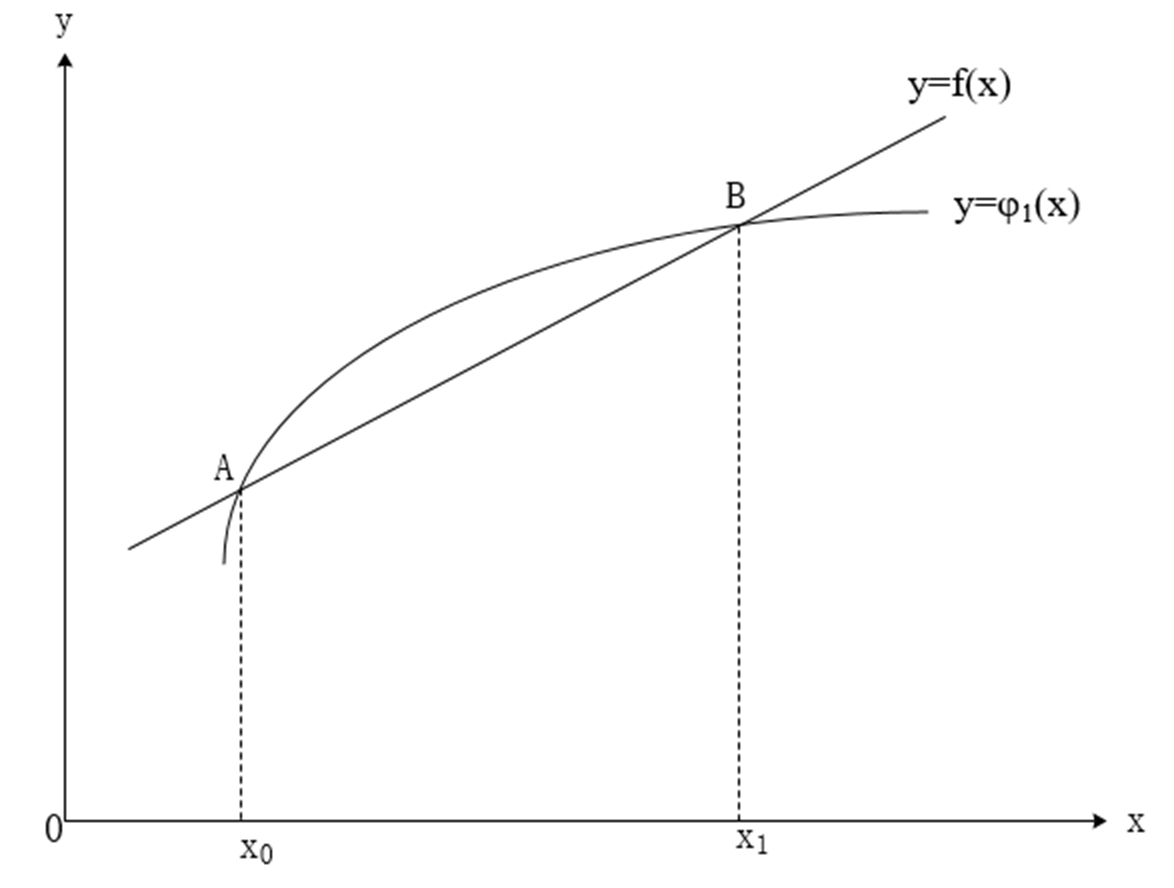
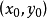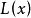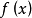線性插值是指插值函式為一次多項式的插值方式,其在插值節點上的插值誤差為零。線性插值相比其他插值方式,如拋物線插值,具有簡單、方便的特點。線性插值的幾何意義即為概述圖中利用過A點和B點的直線來近似表示原函式。線性插值可以用來近似代替原函式,也可以用來計算得到查表過程中表中沒有的數值。
基本介紹
- 中文名:線性插值
- 外文名:Linear Interpolation
- 定義:插值函式為一次多項式的插值方式
- 特點:簡單、方便
- 幾何意義:用過兩插值節點的直線近似原函式
- 套用:近似代替原函式、插值得到數值
基礎知識
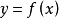





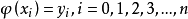



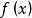


簡介

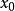





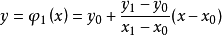

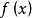
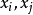
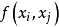
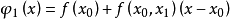
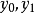
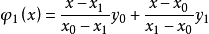
幾何意義