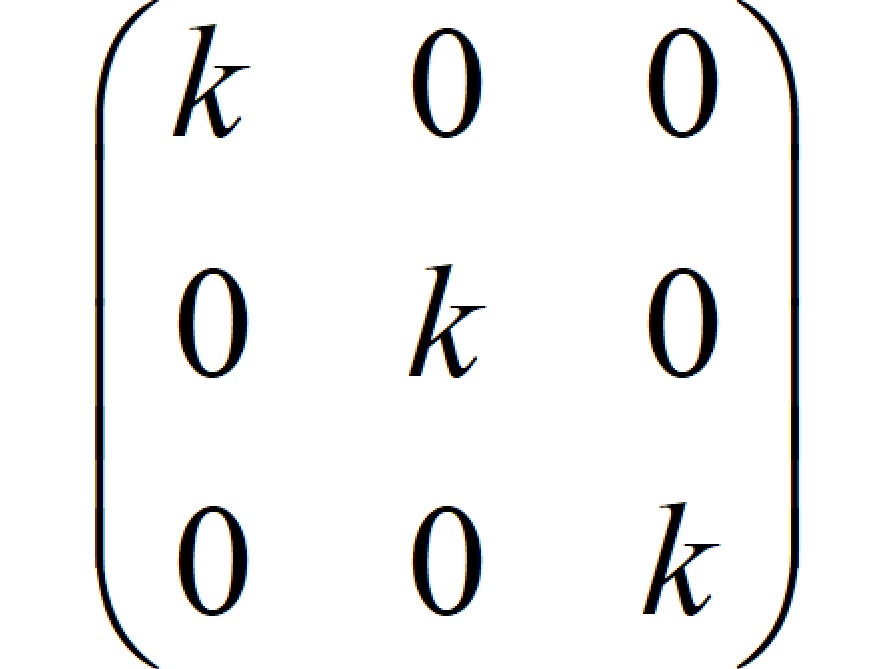基本介紹
- 中文名：純量矩陣
- 外文名：scalar matrix
- 別稱：數量矩陣、標量矩陣、純量陣
- 學科：數學
- 釋義：主對角線元素相同，其餘元素為0
- 性質：有且只有一個n重特徵值
定義,性質,定理1,定理2,定理3,引理及定理,引理,定理,
定義
矩陣A正好是在
的任一基中對應於比為k 的
的同位相似的矩陣。
映射k↦kE是從交換體K到全體n階純量矩陣之集上的同構。
性質
定理1
設A是數域F上n階矩陣，則下列命題等價：
(1) A是純量矩陣；
(2) A與F上任一n階矩陣都可換；
(3) A的任一相似陣必是A本身；
(4) 設
(
表示 i 行 j 列的元素為1，其餘元素全為0的n階矩陣，)；
(5) 設
同(4)，則
；
(6) 設n階矩陣：
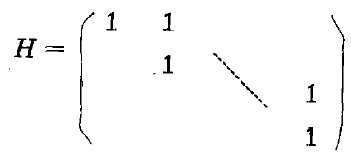
則：AH=HA，AH'=H'A（H'為H的轉置矩陣）；
(7) 設n階矩陣：
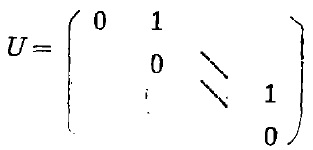
則：AU=UA，AU'=U'A（U'為U的轉置矩陣）；
(8)設n階矩陣U同(7)且：
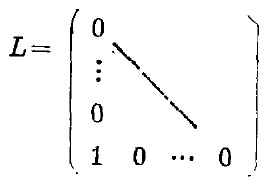
則：AU=UA，AL=LA；
(9)設n階矩陣U同(7)，且：
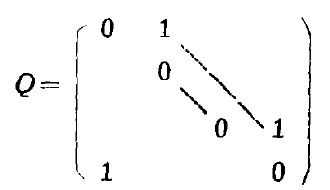
則：AU=UA，AQ=QA。
定理2
設A是數域F上n階矩陣，則下列命題等價：
(1) A是純量矩陣；
(2) A的極小多項式是一次的；
(3) A的不變因式都相等；
(4) A的不變因式都是一次的；
(5) A的行列式因子組是型如
；
(6) A的初等因子全相等，且因子個數等於n；
(7) A的初等因子全相等，且A的初等因子全體等於A的不變因子全體。
定理3
設A是數域F上n階矩陣，V是F上n維向量空間，線性變換A在基下的對應陣是A，則下列命題等價：
(1) A是純量矩陣；
(2) A是純量變換，
即(
，
是V的恆等變換)；
(3) 設B是V的任一線性變換，則AB=BA；
(4) A在V的任一基下所對應的矩陣仍是A；
(5) V的任一子空間都是A的不變子空間；
(6) V的任一一維子空間都是A的不變子空間；
(7) 設V的基為
，則
都是A的不變子空間；
都是A的不變子空間。
引理及定理
引理
引理 1：如果數域F 上 n 階方陣A 與任意n階方陣的乘法是可交換的，那么 A 一定是純量矩陣。
引理 2：數域F 上 n 階方陣A 為純量矩陣的充要條件是 A 與任何 n 階可逆矩陣的乘法可交換。
定理
（1）定理 1：數域F 上 n 階方陣 A 為純量矩陣的充分必要條件是：A 與所有行列式為 1 的n階矩陣可交換。
（2）定理 2：數域 F 上 n 階方陣 A 為純量矩陣的充分必要條件是
中的每個非零向量都是它的特徵向量。
（3）定理 3：數域 F 上 n 階方陣 A 為純量矩陣的充分必要條件是 A 的不變因子都不是常數。
根據定理 3 和行列式因子、初等因子、不變因子的關係，容易得到：
1）推論 1：數域 F 上 n 階方陣 A 為純量矩陣的充分必要條件是 A 的不變因子都是一次的。
2）推論 2：數域 F 上 n 階方陣 A 為純量矩陣的充分必要條件是 A 的 k 階行列式因子都是 k 次的。
3）推論 3：數域 F 上 n 階方陣 A 為純量矩陣的充分必要條件是 A 的初等因子都相等，且 A 的初等因子組
為 A 的不變因子全體。
數域 F 上 n 階矩陣的相似是一個等價關係，在相似關係下， A 的等價類稱為 A 的相似類。
（4）定理 4：數域 F 上 n 階方陣 A 為純量矩陣的充分必要條件是 A 的相似類里只有一個元素。
