基本介紹
定義
例子

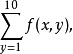
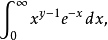
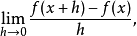
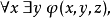
變數約束運算元
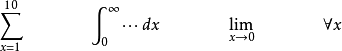
形式解釋
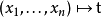


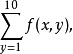
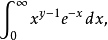
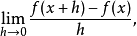
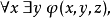
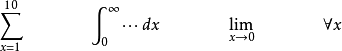
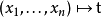
量化一個合式公式中的某個變數所得到的表達式也是合式公式。如果一個合式公式中某個變數是經過量化的,就把這個變數叫做約束變數,否則就叫它為自由變數。在合式...
在數學規劃中,對於決策方案的各項限制,常以不等式或方程式的形式出現。在經濟問題中,對目標函式常常要在一定約束條件下求最大值(或最小值),它們包含著用來代表...
起作用約束(active constraint)亦稱緊約束或積極約束,是指在某可行點處使不等式約束成為等式的約束。對於可行點x',當gi(x')=0時點x'處於這個約束形成的可行域...
簡介 預測控制中無論是單變數還是多變數情況,都沒有考慮系統中存在的約束二然而在實際工業過程中,系統的輸出量和控制量都應約束在一定範圍內.因此,在多變數預測...
約束滿足問題(CSPs)是種數學的問題,其定義為一組對象(object),而這些對象需要滿足一些限制或條件。...
邏輯變數之間的約束關係稱為約束。把不允許出現的對應組合對應的最小項稱為約束項。 ...
在數學中,約束是一個最佳化問題的解需要符合的條件。約束可分為等式約束及不等式約束。符合所有約束的解的集合稱為可行集(feasible set)或是候選解(candidate ...
CSP(約束滿足問題):由一個變數集合和一個約束集合組成。問題的一個狀態是由對一些或全部變數的一個賦值定義的完全賦值:每個變數都參與的賦值。問題的解是滿足所有...
約束最佳化(Constrained Optimization),即約束最佳化問題,是最佳化問題的分支。它是在一系列約束條件下,尋找一組參數值,使某個或某一組函式的目標值達到最優。其中約束...
線上性規劃問題的單純形法中,若標準化後找不到單位矩陣,可以採用人造基,給方程加入人工變數後,用大M法和兩階段法處理求解。是求解線性規劃問題的一種方式。...
決策變數(decision variable)又稱控制變數,設計變數,操作變數等。在描述過程系統的所有變數中,決策變數可以由設計人員按照最能符合系統的目標選擇適當的數值,用來描述...
一個謂詞公式如果其中由一部分公式形如∀xA或∃xA,則凡在這部分中變元x的一切出現都叫做x在此謂詞公式中約束出現,而變元x叫此謂詞公式中的約束變元。一個...
變數化VGX的全稱為variational Geometry Extended,即超變數化幾何,它是由SDRC公司獨家推出的一種CAD軟體的核心技術,我們在進行機械設計和工藝設計時,總是希望零部件...
約束最佳化問題(亦譯為受約束的最最佳化問題)是一類數學最最佳化問題,它由目標函式以及與目標函式中的變數相關的約束條件兩部分組成,最佳化過程則為在約束條件下最最佳化(最...
約束傳播是約束規劃成功套用的關鍵技術之一。針對累積調度問題可提出一種結合工作間優先關係和工作最早開始/最晚完成時間約束的約束傳播算法,保證算法的理論依據。...
《約束力學系統動力學》是2009年出版的圖書。...... 動力學代數與Poisson方法、正則變換、Hamilton-Jacobi方法、場方法、積分不變數;第六部分:約束力學系統的對稱性與...
帶有約束條件的極值問題稱為約束極值問題,也叫規劃問題。若某非線性規劃的目標函式為自變數x的二次函式,約束條件又全是線性的,就稱這種規劃為二次規劃。...
絕對約束環境是指必須嚴格滿足的等式或不等式約束的求解環境。如線性規劃問題中的所有約束條件都是絕對約束,線性規劃問題的求解環境就是絕對約束環境。...
《多變數控制約束映射與約束預測控制相關問題研究》是張惜嶺撰寫的一篇論文,收藏於中國國家圖書館。...
因變數(dependent variable)函式中的專業名詞,也叫函式值。函式關係式中,某些特定的數會隨另一個(或另幾個)會變動的數的變動而變動,就稱為因變數。如:Y=f(X...
側面約束不針對性能要求,只是對設計變數的取值範圍加以限制的約束稱作側面約束。 側面約束也稱作邊界約束。側面約束套用針對安全法規關於不同碰撞形態下對乘員側面保護...
