基本介紹
- 中文名:自由變數
- 外文名:Free variable
- 義項1:線性規劃中無非負限制的變數
- 義項2:指在公式中有自由出現的變數
- 所屬學科:數學
線性規劃中的自由變數,謂詞公式中的自由變數,
線性規劃中的自由變數
自由變數(free variable)是指線性規劃中沒有非負性條件的設計變數。若問題中含有這種變數,為構成線性規劃標準式,常以兩個相減的非負設計變數替代之,使最佳化設計數學模型中的所有設計變數均為非負設計變數。替代前後的最優解是等價的。具有自由變數的線性規劃問題有時亦可利用對偶理論化為對偶問題直接求解。
自由變數線上性規劃問題數學模型中,如果出現沒有非負限制,可以為正,也可以為負的變數 就稱其為自由變量。化標準形時,需引進兩個非負變數
就稱其為自由變量。化標準形時,需引進兩個非負變數 ,
, ,令
,令 將自由變數轉化為有非負要求約束的變數。
將自由變數轉化為有非負要求約束的變數。




各種線性規劃模型都需要轉化成標準型後求解。下面介紹各種轉化方法。
(1)最小化問題的轉化。求min z等價於求max(-z),因此,只需改變目標函式的符號就可以實現最大化和最小化之間的轉換。

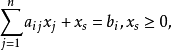


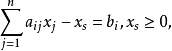

(3)非正變數與符號無限制變數的處理。
若 ,令
,令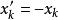 ,則新變數
,則新變數 為非負變數。
為非負變數。

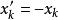

若 為符號無限制變數(稱為自由變數),可令
為符號無限制變數(稱為自由變數),可令 ,即以兩個非負變數之差來代替自由變數。
,即以兩個非負變數之差來代替自由變數。


從以上討論可見,任何形式的線性規劃都可轉化為標準型。
謂詞公式中的自由變數
通常稱變數x在謂詞公式 和
和 中的出現為約束出現; 並稱A為
中的出現為約束出現; 並稱A為 和
和 的作用域(或轄域)。如果變數x在公式A中的某次出現是在A的分子公式中的約束出現,則稱x的該次出現是約束出現;若變數x在公式A的某次出現不是約束出現,就稱該出現為自由出現。 在公式A中有自由出現的變數稱為自由變數,在公式A中有約束出現的變數稱為約束變數。
的作用域(或轄域)。如果變數x在公式A中的某次出現是在A的分子公式中的約束出現,則稱x的該次出現是約束出現;若變數x在公式A的某次出現不是約束出現,就稱該出現為自由出現。 在公式A中有自由出現的變數稱為自由變數,在公式A中有約束出現的變數稱為約束變數。




例如,謂詞公式 ,從左向右算起,變數x的第一、二、三次出現是約束出現,第四次出現是自由出現,變數
,從左向右算起,變數x的第一、二、三次出現是約束出現,第四次出現是自由出現,變數 則全是自由變數。
則全是自由變數。


可以看出,一個變數可以既是約束變數,又是自由變數。
顯然,公式 和公式
和公式 的真值相同,同樣, 公式
的真值相同,同樣, 公式 和公式
和公式 的真值也相同。也即,謂詞邏輯中的謂詞的真值與謂詞中的約束變數的記法無關。因此,可引入改名規則:若打算把某謂詞公式中的量詞(Qx)換成(Qy),則y必須是在該(Qx)的作用域內不出現的變數,並且把該(Qx)的作用域內一切自由出現的x換成y。(其中,Q為
的真值也相同。也即,謂詞邏輯中的謂詞的真值與謂詞中的約束變數的記法無關。因此,可引入改名規則:若打算把某謂詞公式中的量詞(Qx)換成(Qy),則y必須是在該(Qx)的作用域內不出現的變數,並且把該(Qx)的作用域內一切自由出現的x換成y。(其中,Q為 或
或 )
)






例如,對於 可改名為
可改名為 。
。


用x\p來表示“變數x在p中不是自由的”。如果x\p且x\q,那么在複合公式 中,x也不是自由變數。當變數在集合表達式中聲明時,它總為約束變數。例如:
中,x也不是自由變數。當變數在集合表達式中聲明時,它總為約束變數。例如:




