系統聚類法（hierarchical cluster method）一譯“分層聚類法”。聚類分析的一種方法。其做法是開始時把每個樣品作為一類，然後把最靠近的樣品（即距離最小的群品）首先聚為小類，再將已聚合的小類按其類間距離再合併，不斷繼續下去，最後把一切子類都聚合到一個大類。
基本介紹
- 中文名：系統聚類法
- 外文名：hierarchical cluster method
- 別稱：分層聚類法
- 類型：聚類分析
- 算法：中間距離法、重心法
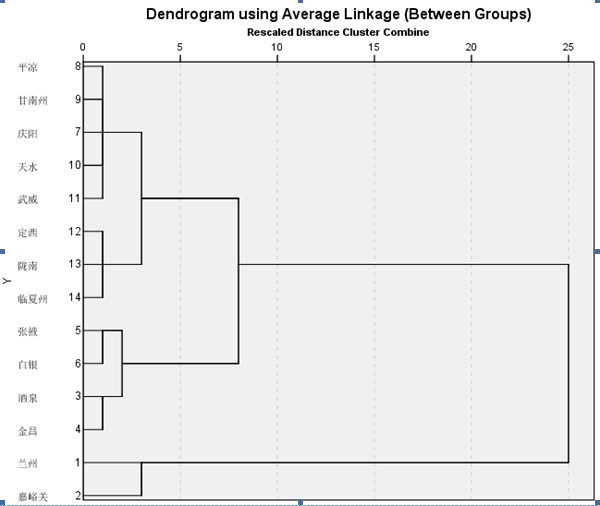
- 關鍵：生成聚類圖
步驟,基本思想,常用方法,
步驟
以n個樣本的聚類分析為例，系統聚類法的步驟如下：
定義以變數或指標的個數為維度的空間裡的一種距離；
計算n個樣本兩兩之間的距離；
將每個樣本歸為一類，根據計算出的樣本間的距離合併距離最近的兩類為一個新類；
再計算新類與其他各類的距離，同樣再根據計算出的距離合併距離最近的兩類為一個新類；
循環以上過程直至類別個數為1；
畫出各階段的聚類圖並決定類別的個數。
對於變數聚類分析，只需要將距離替換為相似係數，然後將相似係數較大的變數分別聚類即可。
基本思想
系統聚類法是目前國內外使用得最多的一種聚類方法，這種方法是先將聚類的樣本或變數各自看成一群，然後確定類與類間的相似統計量，並選擇最接近的兩類或若干個類合併成一個新類，計算新類與其他各類間的相似性統計量，再選擇最接近的兩群或若干群合併成一個新類，直到所有的樣本或變數都合併成一類為止。
首先將幾個樣品各自作為一類，並規定樣品之間的距離和類與類之間的距離，然後將距離最近的兩類合併成一個新類，計算新類與其他類的距離；重複進行兩個最近類的合併，每次減少一類，直至所有的樣品合併成一類。
常用方法
確定了距離和相似係數後就要進行分類。分類有許多種方法，最常用的一種方法是在樣品距離的基礎上定義類與類之間的距離。首先將n個樣品分成n類，每個樣品自成一類，然後每次將具有最小距離的兩類合併，合併後重新計算類與類之間的距離，這個過程一直持續到將所有的樣品歸為一類為止，並把這個過程畫成一張聚類圖，參照聚類圖可方便地進行分類。因為聚類圖很像一張系統圖，所以這種方法就叫系統聚類法。系統聚類法是目前在實際中使用最多的一種方法，從上面的分析可以看出，雖然我們已給了計算樣品之間距離的方法，但在實際計算過程中還要定義類與類之間的距離。定義類與類之間的距離也有許多方法，不同的方法就產生了不同的系統聚類方法，常用的有如下六種：
(1)最短距離法：類與類之間的距離等於兩類最近樣品之間的距離；
(2)最長距離法：類與類之間的距離等於兩類最遠樣品之間的距離：
(3)類平均法：類與類之問的距離等於各類元素兩兩之間的平方距離的平均；
(4)重心法：類與類之間的距離定義為對應這兩類重心之間的距離對樣品分類來說，每一類的類重心就是該類樣品的均值；
(5)中間距離法：最長距離法誇大了類間距離，最短距離法低估了類間距離介於兩者問的距離法即為中間距離法，類與類之問的距離既不採用兩類之間最近距離。也不採用最遠距離，而是採用介於最遠和最近之間的距離；
(6)離差平方和法(Ward法)：基於方差分析的思想，如果分類正確，同類樣品之間的離差平方和應當較小，類與類之間的離差平方和應當較大。
