基本介紹
- 中文名:米勒-拉賓素性檢驗
- 外文名:Miller-Rabin prime test
- 定義:素數判定法則
- 相關術語:隨機化算法
- 學科:密碼學
- 領域:密碼學
概念,例子,算法複雜度,
概念


現在假設n是一個奇素數,且 n>2。於是n-1是一個偶數,可以被表示為 的形式,s和d都是正整數且d是奇數。對任意在
的形式,s和d都是正整數且d是奇數。對任意在 範圍內的a 和
範圍內的a 和 ,必滿足以下兩種形式的一種:
,必滿足以下兩種形式的一種:







米勒-拉賓素性測試就是基於上述原理的逆否,也就是說,如果如果我們能找到這樣一個a,使得對任意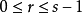 以下兩個式子均滿足:
以下兩個式子均滿足:
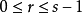


每個奇合數n都有很多個對應的憑證a,但是要生成這些a並不容易。當前解決的辦法是使用機率性的測試。我們從集合 中隨機選擇非零數a,然後檢測當前的a是否是n為合數的一個憑證。如果n本身確實是一個合數,那么大部分被選擇的a都應該是n的憑證,也即通過這個測試能檢測出n是合數的可能性很大。然而,仍有極小機率的情況下我們找到的a是一個“強偽證”(反而表明了n可能是一個素數)。通過多次獨立測試不同的a,我們能減少這種出錯的機率。
中隨機選擇非零數a,然後檢測當前的a是否是n為合數的一個憑證。如果n本身確實是一個合數,那么大部分被選擇的a都應該是n的憑證,也即通過這個測試能檢測出n是合數的可能性很大。然而,仍有極小機率的情況下我們找到的a是一個“強偽證”(反而表明了n可能是一個素數)。通過多次獨立測試不同的a,我們能減少這種出錯的機率。

對於測試一個大數是否是素數,常見的做法隨機選取基數a,畢竟我們並不知道憑證和偽證在 [1,n-1]這個區間如何分布。典型的例子是 Arnault 曾經給出了一個397位的合數n,但是所有小於307的基數a都是n是素數的“強偽證”。不出所料,這個大合數通過了 Maple 程式的isprime()函式(被判定為素數)。這個函式通過檢測 a=2,3,5,7,11這幾種情況來進行素性檢驗。
例子
假設我們需要檢驗n=221是否是一個素數。首先 ,於是我們得到了 s=2和d=55。我們隨機從[1,n-1]中選取a,假設a=174,於是有:
,於是我們得到了 s=2和d=55。我們隨機從[1,n-1]中選取a,假設a=174,於是有:





算法複雜度
這一算法可以被表示成如下偽代碼:
Input #1: n > 3, an odd integer to be tested for primality;
Input #2: k, a parameter that determines the accuracy of the test
Output: composite if n is composite, otherwise probably prime
write n − 1 as 2r·d with d odd by factoring powers of 2 from n − 1
WitnessLoop: repeat k times:
pick a random integer a in the range [2, n − 2]
x ← ad mod n
if x = 1 or x = n − 1
then
continue WitnessLoop
repeat r − 1 times:
x ← x2 mod n
if x = 1
then
return composite
if x = n − 1
then
continue WitnessLoop
return compositereturn probably prime
使用模冪運算,這個算法的時間複雜度是 ,k是我們測試的不同的a的值。也就是說,這是一個高效的多項式時間算法。使用快速傅立葉變換能夠將這個時間推進到O(klognlog lognlog log logn) =Õ(klogn).
,k是我們測試的不同的a的值。也就是說,這是一個高效的多項式時間算法。使用快速傅立葉變換能夠將這個時間推進到O(klognlog lognlog log logn) =Õ(klogn).

如果我們加入最大公因數算法到上述算法中,我們有時候可以得到n的因數,而不僅僅是證明n是一個合數。例如,若n是一個基於a的可能的素數,但不是一個大機率素數,則 或
或 將得到n的因數。如果因式分解是必要的,這一GCDs算法可以加入到上述的算法中,代價是增加了一些額外的運算時間。
將得到n的因數。如果因式分解是必要的,這一GCDs算法可以加入到上述的算法中,代價是增加了一些額外的運算時間。


例如,假設n=341,則n-1=340=85*4。於是 ,這也告訴我們n不是一個大機率素數,即n是一個合數。如果這個時候我們求最大公因數,我們可以得到一個n=341的因數:
,這也告訴我們n不是一個大機率素數,即n是一個合數。如果這個時候我們求最大公因數,我們可以得到一個n=341的因數: 。這是時可行的,因為n=341是一個基於2的偽素數,但不是一個“強偽素數”。
。這是時可行的,因為n=341是一個基於2的偽素數,但不是一個“強偽素數”。







