基本介紹
- 中文名:簡單對數不等式
- 外文名:simple logarithmic inequality
- 別稱:最簡對數不等式
- 所屬學科:數學
- 所屬問題:初等代數(不等式)
基本概念


對數不等式的解法












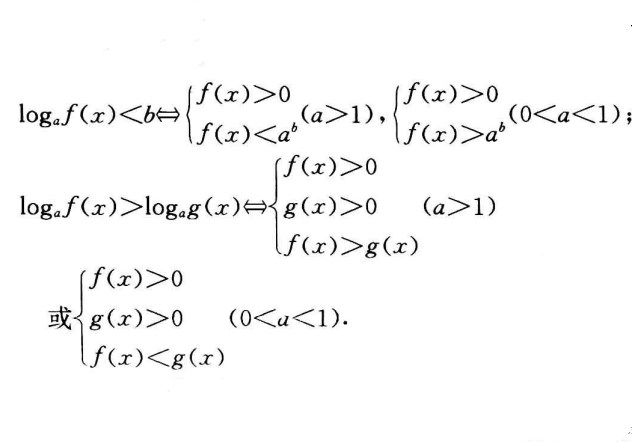














簡單對數不等式(simple logarithmic inequality)亦稱最簡對數不等式,是一種常見的對數不等式,形如logax0,a≠1)或logax>b(a>0,a≠1)以及logaf(x)<log...
簡單指數不等式(simple exponential inequality)亦稱最簡指數不等式,是一種常見的指數不等式,即形如ax0,a≠1),ax>b(a>0,a≠1)的不等式。...
對數不等式是一種兩邊由對數構成的不等式。...... 對數不等式化同底或換元法 若logaf(x)1時,原不等式化為當0<a<1時,原不等式化為.“分段函式型”不等式...
簡單對數方程的解法步驟如下 [2] :①化指法;②同底法;③換元法;...先由不等式組 確定方程中的 的取值範圍,然後把原方程化為 ,求出在此範圍內...
對數函式、三角函式等;最後,運用函式的思想方法討論了涉及不等式以及數列的簡單問題.通過本冊書的學習,體會數學中描述變數之間的關係,感悟通過建立數學模型來刻畫和...
第二節 無理不等式和絕對值不等式的解法 第三節 指數不等式與對數不等式的解法...第十章 簡單多面體與球 第十一章 特殊四面體 第十二章 排列與組合 第十三章 ...
3.7 簡單的函式方程第四章 冪函式、指數函式、對數函式4.1 冪函式4.2 指數函式4.3 對數概念及其運算4.4 反函式4.5 對數函式4.6 指數方程和指數不等式...
第二節 簡單的三角方程 第五章 不等式 第一節 不等式的性質 第二節 一元一次...第四節 無理不等式的解法 第五節 指數不等式與對數不等式的解法 第六節 含...
對數函式、三角函式等;最後,運用函式的思想方法討論了涉及不等式以及數列的簡單問題.通過本冊書的學習,體會數學中描述變數之間的關係,感悟通過建立數學模型來刻畫和...
幾種簡單的對數方程及其解法 五、冪函式 冪函式的概念 冪函式的圖像與性質 函式的最值 求函式最值的常用方法 易錯題辨析 第三部分不等式 一、不等...
