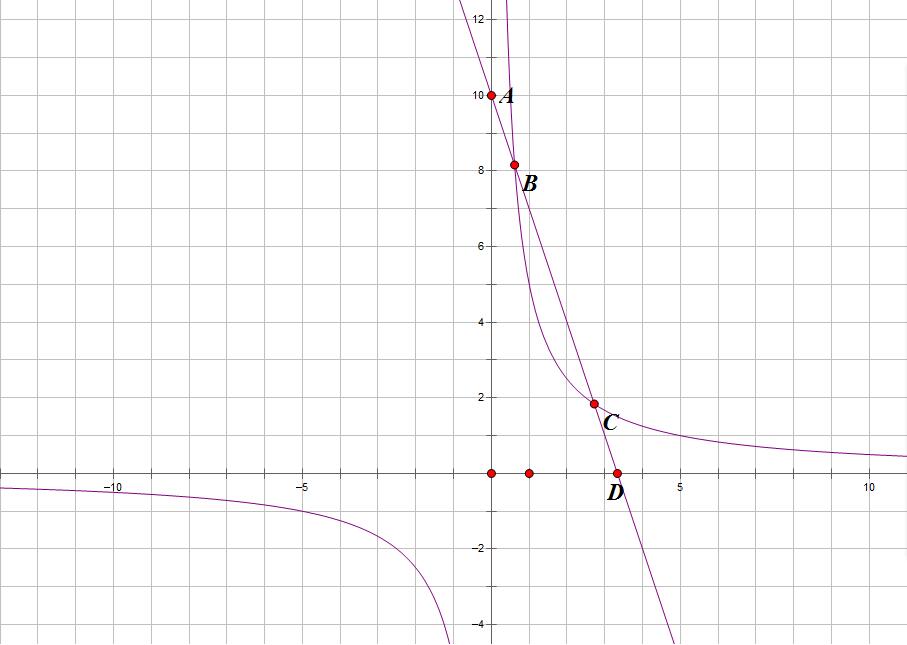
如圖所示,在直角坐標系中,有反比例函式y=k1/x與直線y=k2x+b有兩個交點,分別為B,C,且直線y=k2x+b與坐標軸交與兩點,分別為A,D。(註:不僅交點在第一象限,其他象限也可以,A,B,C,D坐標不一定如圖中所示,後面給予證明可知只要這兩個函式圖像有交點,相切時也成立,後面給出。)
則AB=CD。
也可得AC=BD。
基本介紹
- 中文名:等距定理
- 提出者:琉璃
- 提出時間:2018年6月18日
- 適用領域:平面直角坐標系
- 套用學科:數學
定律定義
推導過程

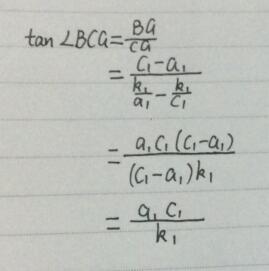
第二種情況
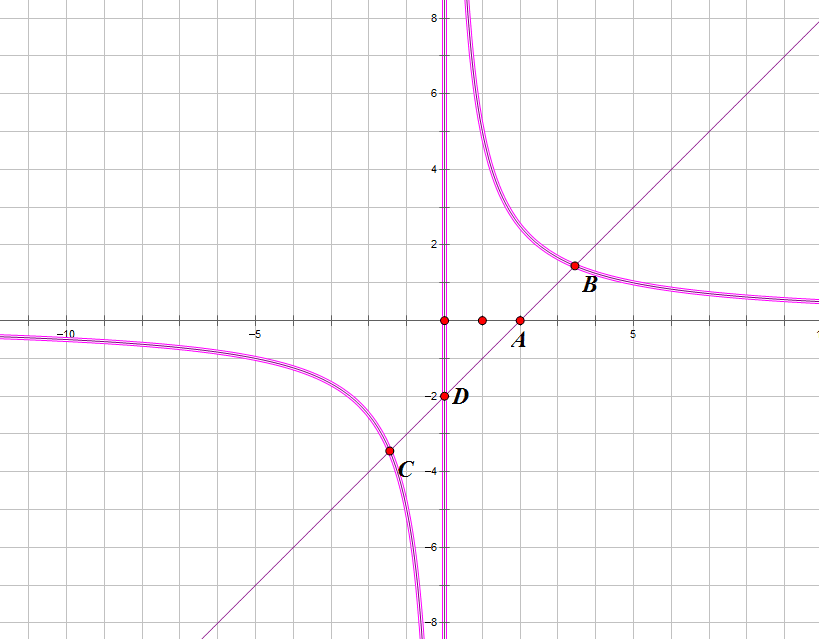

相切成立

演算過程
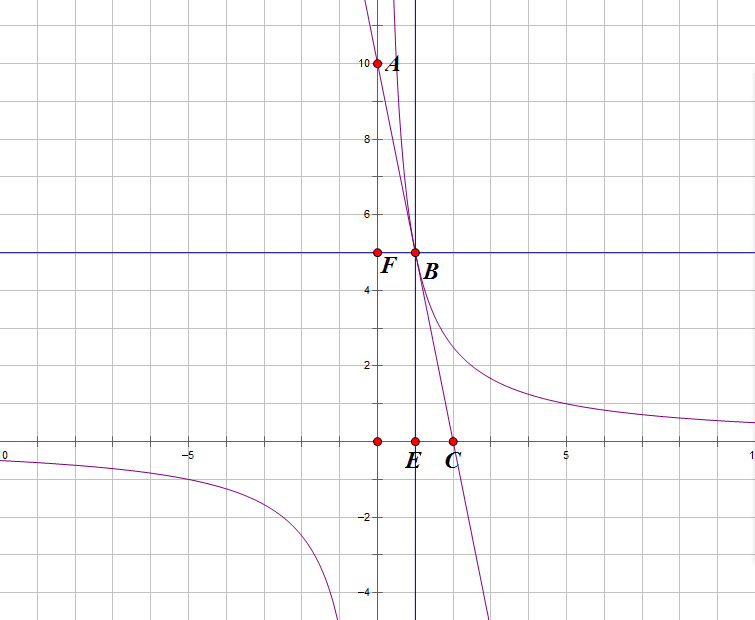

如圖所示,在直角坐標系中,有反比例函式y=k1/x與直線y=k2x+b有兩個交點,分別為B,C,且直線y=k2x+b與坐標軸交與兩點,分別為A,D。(註:不僅交點在第一象限,其他象限也可以,A,B,C,D坐標不一定如圖中所示,後面給予證明可知只要這兩個函式圖像有交點,相切時也成立,後面給出。)
則AB=CD。
也可得AC=BD。


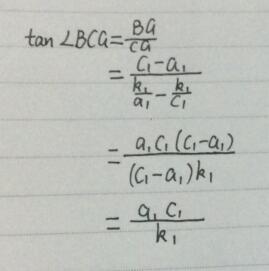




如圖所示,在直角坐標系中,有反比例函式y=k1/x與直線y=k2x+b有兩個交點,分別為B,C,且直線y=k2x+b與坐標軸交與兩點,分別為A,D。(註:不僅交點在第一象限,其他象限也可以,A,B,C,D坐標不一定如圖中...
實內積空間上的等距同構通常稱為正交(orthogonal)運算元.復內積空間上的等距同構通常稱為酉(unitary) 運算元.我們將採用等距同構這個術語,因此我們的結果對於實內積空間和復內積空間都可用.相關性質與定理 定義1 如果度量空間(N2,ρ2)的...
最大直徑定理(maximal diameter theorem )是關於正曲率流形與同維球面等距的定理。設M是n維完備黎曼流形,其里奇曲率(n-1)H0,其中H是常數.若它的直徑等於耐、儷,,則M必與Rn+中半徑為1/的球面sn y l!等距.上述定理是鄭紹遠證明...
=CD CE'=AE AF'=BF 則AD' BE' CF'三線交於一點Q,則稱Q與P互為等距共軛點。三線共點的證明:BD'/D'C*CE'/E'A*AF'/F'B=BD/DC*CE/EA*AF/FB 由Ceva定理AD',BE',CF'三線共點。
因為如果有兩個不動點,例如說是A和B,那么會產生一條不動的線段AB,因為k=AB/AB=1,所以這個相似變換就是保持兩點固定的等距變換。如果這個變換把△ABC變為△ABC',我們能把C'安於中心在A和B,半徑為AC和BC的兩個圓上。這樣...
沃爾德分解(Wold decomposition)寬平穩過程的一種分解表示。.簡介 在數學中,特別是在運算元理論中,沃爾德分解或Wold-von Neumann分解(以Herman Wold和John von Neumann命名)是給定希爾伯特空間上等距線性運算元的分類定理。它指出,每一個等距...
黎曼流形的整體等距嵌入定理於1954~1956年由J.納許等所給出:n 維黎曼流形總可等距嵌入到歐氏空間E,如流形為緊緻時,則可嵌入到E;如果只考慮C1等距嵌入,則n維黎曼流形可嵌入於;如果M緊緻則可嵌入到。納許的方法後來對非線性分析...
但是在不同的領域中,“完備”也有不同的含義,特別是在某些領域中,“完備化”的過程並不稱為“完備化”,另有其他的表述,請參考代數閉域、緊化(compactification)或哥德爾不完備定理。直觀上講,一個空間完備就是指“沒有孔”且“...
相關定理 巴拿赫定理:對任意巴拿赫空間 ,都存在緊豪斯多夫空間X,使得 等距同構於C(X)的閉子空間。開映射定理 閉圖像定理 例子 巴拿赫空間有兩種常見的類型:“實巴拿赫空間”及“復巴拿赫空間”,分別是指將巴拿赫空間的向量空間定義於...
相關定理 Gelfand-Naimark定理 定義 設A為含麼元的交換C*代數,X=sp(A)為其蓋爾范德譜。則蓋爾范德映射Γ為A到C(X)的等距*同構。推導 A中元T=H+iK,其中H與K均為自伴元,故擁有實譜,故Γ(H)與Γ(K)為實的。故有 故Γ...
維特定理 在數學中,維特定理以厄恩斯特維特(Ernst Witt)命名而來,是二次形式的代數理論的基本定理:域k上的非奇異二次空間的兩個子空間之間的任何等值線可以擴展到整個空間的等距。 類似的聲明也適用於任意領域的偏斜對稱,Hermitian...
但是在不同的領域中,“完備”也有不同的含義,特別是在某些領域中,“完備化”的過程並不稱為“完備化”,另有其他的表述,請參考代數閉域、緊化(compactification)或哥德爾不完備定理。直觀上講,一個空間完備就是指“沒有孔”且“...
相關定理 Gelfand-Naimark定理 定義 設A為含單位元的交換C*代數,X=sp(A)為其蓋爾范德譜。則蓋爾范德映射Γ為A到C(X)的等距*同構。推導 A中元T=H+iK,其中H與K均為自伴元,故擁有實譜,故Γ(H)與Γ(K)為實的。故有 故...
4.2 等距對應:共形映照 4.3 Gauss定理和相容性方程 4.4 平行移動;測地線 4.5 Gauss-Bonnet定理及其套用 4.6 指數映照;測地極坐標 4.7 測地線的一些進一步的性質;凸鄰域 附錄 曲線自由式面局部理論經基本定的證明 第5章 ...
3.3 Hahn-Banach定理的延拓 第4章 Hahn-Banach定理的套用 4.1 正線性泛函的延拓 4.2 Banach極限 4.3 有限可加的不變集函式 第5章 賦范線性空間 5.1 範數 5.2 單位球的非緊性 5.3 等距 第6章 Hilbert空間 6.1 內積...
另一方面,Ebin發現了關於緊黎曼流形的黎曼結構形變時相應的等距群本身有某種“半連續性”。受Ebin的定理的啟發,作者打算研究關於緊複流形的復結構形變時,相應的全純自同構群本身的的“半連續性”定理,這種“半連續性”定理可看作...
Artin的主要貢獻包括他的逼近定理、在解決沙法列維奇-泰特猜測中的工作以及為推廣“概形”而創建的“代數空間”概念。目錄 譯者序 前言 記號 章 矩陣 節 基本運算 第二節 行約簡 第三節 矩陣的轉置 第四節 行列式 ...
