基本介紹
- 中文名:等角對等邊
- 外文名:sides opp. equal angles
- 學習:人教版八年級上冊數學
- 學科:數學
等角對等邊
等角對等邊的證明方法
證法一
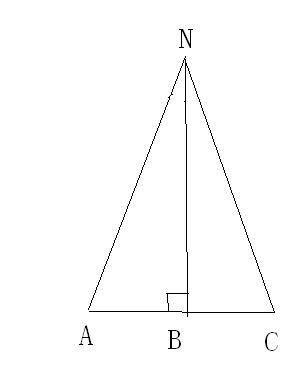 “等角對等邊”性質
“等角對等邊”性質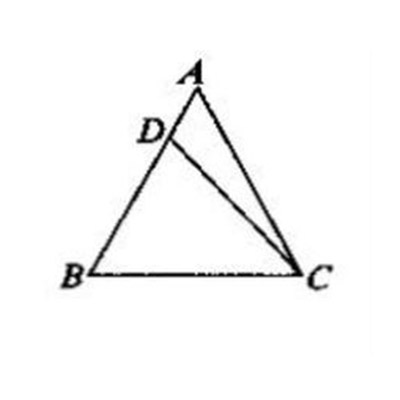
 “等角對等邊”性質
“等角對等邊”性質在同一三角形中,如果兩個角相等,那么這兩個角所對的邊也相等。通常用來證明等腰三角形。(等邊對等角的逆定理)等角對等邊的性質在人教版八年級上冊數學第十五章...
等角顧名思義就是相等的角,即角度大小相等的角。...... 概念 角度大小相等的角 性質 等角的餘角相等 性質 等角對等邊 目錄 1 等角的性質 2 關於等角 等...
逆命題3成立,CD=AD則∠A=∠ACD,而∠A+∠B=90°,∠ACD+∠BCD=90°,因此∠BCD=∠B。等角對等邊,有CD=DB,所以AD=BD,即D是斜邊中點。...
對角,是指在三角形中兩邊所夾的內角稱為第三邊的對角。對角的套用:1、等邊對等角:等腰三角形中,相等的兩腰的對角也相等。2、等角對等邊:三角形中如果兩個...
(3)有一個角是60度的等腰三角形是等邊三角形特殊三角形等腰直角三角形 編輯 特殊三角形定義 等腰直角三角形是一種特殊的三角形,具有所有三角形的性質:穩定性,兩...
等邊三角形的判定:(1)三個內角或三個對應位置的外角都相等的三角形是等邊三角形;(2)有一個角等於60°的等腰三角形是等邊三角形。...
34 等腰三角形的判定定理 如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊)35 推論1 三個角都相等的三角形是等邊三角形...
34.等腰三角形的判定定理 如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊)35.推論1三個角都相等的三角形是等邊三角形...
等角對等邊的聯想 1990年第7期 中學數學 競賽講座 利用二次函式的性質證明不等式 1990年第10期 中學數學 專題研究 從常數中尋找解題思路 1990年第12期 中學...
34 等腰三角形的判定定理 如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊)35 推論1 三個角都相等的三角形是等邊三角形...
34 、等腰三角形的判定定理 :如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊)35、 推論1 :三個角都相等的三角形是等邊三角形...
34 等腰三角形的判定定理 如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊) 35 推論1 三個角都相等的三角形是等邊三角形 36 推論 2 ...
等角對等邊等邊對等角三線合一正弦定理餘弦定理正切定理餘切定理梅涅勞斯定理(及其逆定理)塞瓦定理(及其逆定理)中線定理斯台沃特定理拿破崙定理...
34 等腰三角形的判定定理 如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊)35 推論1 三個角都相等的三角形是等邊三角形...
34 等腰三角形的判定定理 如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(等角對等邊)35 推論1 三個角都相等的三角形是等邊三角形...
