等傾割線(isoclinal secant line)是羅氏平面上的基本曲線之一,與共面二直線a,b相交成相等的同側內角的直線,稱為二直線a,b的等傾割線。在羅氏平面上,共面二直線有相交、平行、離散三種位置關係,過一直線上一定點都存在等傾割線AB,在相交情形有兩條等傾割線AB,AB′,在平行和離散的情形,這樣的割線是惟一的,交點A,B稱為等傾割線的端點。
基本介紹
- 中文名:等傾割線
- 外文名:isoclinal secant line
- 所屬學科:數學
- 所屬問題:高等幾何(非歐幾里得幾何)
- 簡介:羅氏平面上的基本曲線之一
基本概念,相關定理及證明,
基本概念
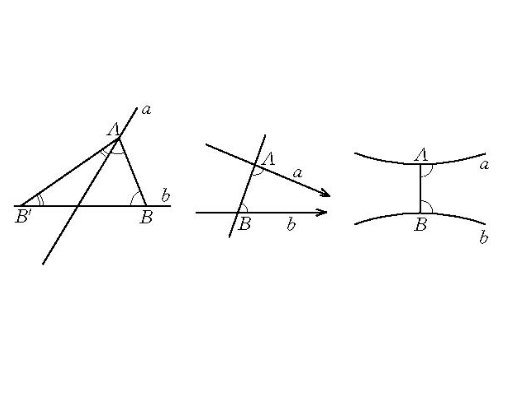
設直線AB與共面兩條直線a,b相交於A,B兩點,若使得同側的內角契約,則稱直線AB為這兩條直線a,b的等傾割線。點A和點B稱為對應點。
相關定理及證明
定理1 設a,b為共面二直線,A為a上一點,則在b上必存在點A的對應點B,且當a,b不交時,A的對應點B是唯一的。
證明: 由表 1 所示:
(1)若a,b交於O,在b上點O之兩側取點B和B',使OA≡OB且OA≡OB’,則線段AB,AB'均為a,b之等傾割線,故B,B'都是A的對應點。
(2)若a,b分散,則有公垂線A'B'。在b上取點B使B'B≡A’A且B與A落在公垂線同側,則四邊形AA'B'B是薩開里四邊形。故∠A'AB≡∠B’BA,所以AB為a,b的等傾割線。從而B為A的對應點。設B”為b上異於B的點,則由三角形外角定理可知:∠B’B”A“≠∠A'AB,所以AB”不是a,b的等傾割線,故B點唯一。
(3)若a,b平行。設平行方向為 ,聯A及b上任一點B0,作AB0所截平行方向一側二內角之平分線,設它們交於點I,作
,聯A及b上任一點B0,作AB0所截平行方向一側二內角之平分線,設它們交於點I,作 於M,作
於M,作 於N,則IM=IN,從而∠AMN≡∠B0NM,在b上取NB≡MA且B與A落在MN同側,則△AMN≡△BMN(邊,角,邊),從而△MAB≡△ABN(邊,邊,邊),所以AB是a,b的等傾割線,故B為A的對應點,其唯一性的證明與(2)同。
於N,則IM=IN,從而∠AMN≡∠B0NM,在b上取NB≡MA且B與A落在MN同側,則△AMN≡△BMN(邊,角,邊),從而△MAB≡△ABN(邊,邊,邊),所以AB是a,b的等傾割線,故B為A的對應點,其唯一性的證明與(2)同。



定理2(等傾傳遞性定理) 若同一線束的三直線a,b,c各通過點A、B、C,且線段AB、AC都是等傾割線,則線段BC也是等傾割線。
證明 (1)當線束有中心O時(見圖1),由於AB、AC都是等傾割線,所以∠OAB≡∠OBA,∠OAC≡∠OCA,從而OA≡OB≡OC所以∠OBC≡∠OCB.故BC也是等傾割線。
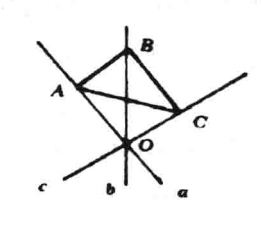 圖1
圖1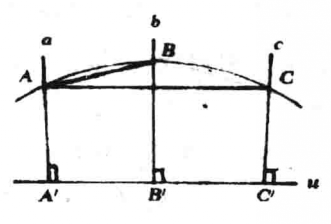 圖2
圖2(2)當線束有底線u時,設A、B、C到u的垂線足各為A'、B’、C’(見圖2)。由於AB、AC都是等傾割線,所以∠A'AB≡∠B'BA,∠A'AC≡∠C'CA,從而AA’≡BB’≡CC’,所以∠B’BC≡∠C’CB,所以BC為等傾割線。
先證 ,
, 在a異側時的情形(見圖3)。
在a異側時的情形(見圖3)。


若BC為非等傾割線,則可設∠BCC'>∠CBB',於是∠C'CB內部有CC1使∠BCC1≡∠CBB',由於 ∥
∥ ,所以
,所以 必交
必交 於一點C1,聯AC1,由於∠B'BA≡∠BAA'>∠BAC1,所以BC1<AC1,又∠C1AC>∠A'AC≡∠ACC’>∠ACC,所以AC1<CC1,故BC1<CC1,但由BCC1≡∠CBB’知BC1=CC1相矛盾。故BC是等傾割線。
於一點C1,聯AC1,由於∠B'BA≡∠BAA'>∠BAC1,所以BC1<AC1,又∠C1AC>∠A'AC≡∠ACC’>∠ACC,所以AC1<CC1,故BC1<CC1,但由BCC1≡∠CBB’知BC1=CC1相矛盾。故BC是等傾割線。




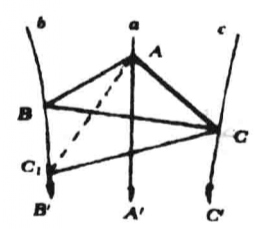 圖3
圖3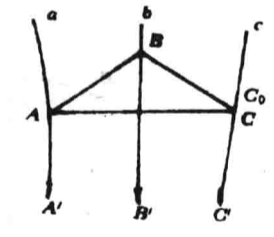 圖4
圖4再證 ,
, 落在a同側時的情形(見圖4)。
落在a同側時的情形(見圖4)。


設b在中間,由定理1知,直線c上有B之對應點C0,由上面已證之情形可知AC0必為等傾割線,即C,C0都是點A的對應點,由定理1知,點A的對應點是唯一的,所以C=C0,即BC為等傾割線。