基本介紹
- 中文名:等值命題
- 外文名:equivalent propositions
- 別名:等價命題、等效命題
- 學科:數學
- 釋義:真假值相同的兩命題
- 性質:原命題與其逆否命題互為等值命題
命題介紹
等值轉換
與相容命題

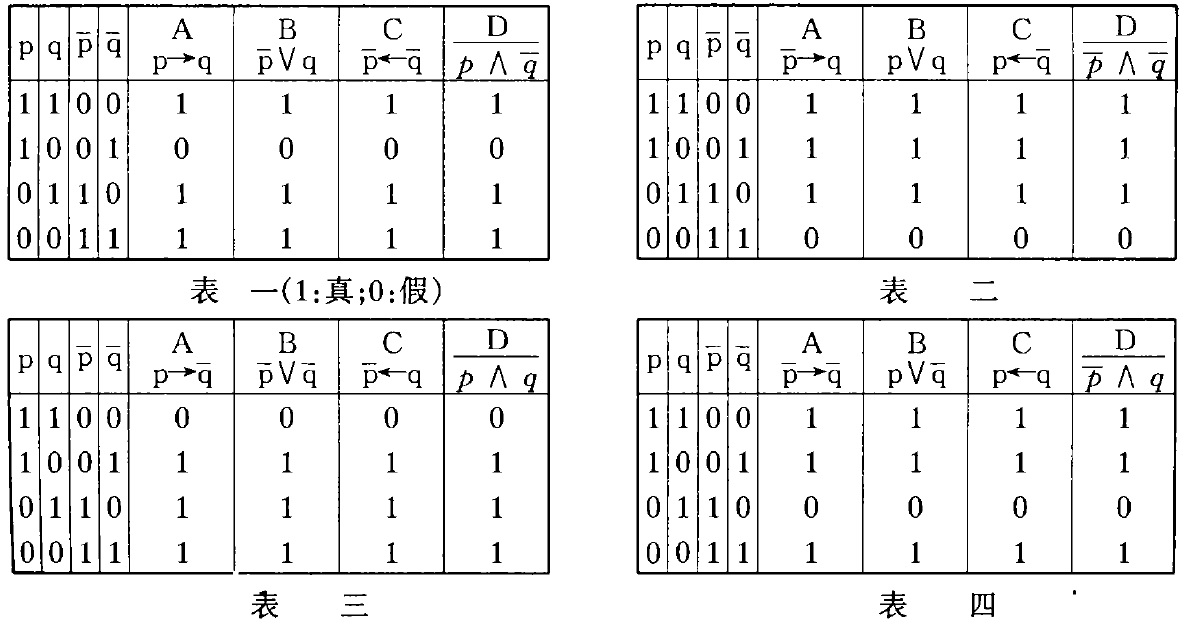



必要假言命題






負聯言命題



選言命題
與充分條件



與必要條件



與負聯言命題




基本理論
定義
關係
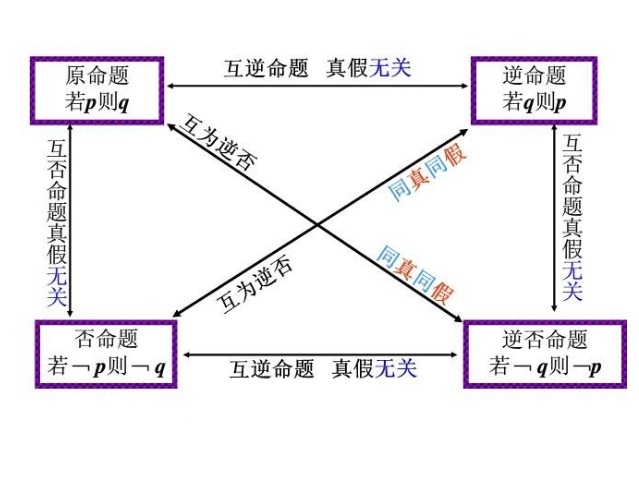
原命題 | 逆命題 | 否命題 | 逆否命題 |
真 | 真 | 真 | 真 |
真 | 假 | 假 | 真 |
假 | 真 | 真 | 假 |
假 | 假 | 假 | 假 |


























原命題 | 逆命題 | 否命題 | 逆否命題 |
真 | 真 | 真 | 真 |
真 | 假 | 假 | 真 |
假 | 真 | 真 | 假 |
假 | 假 | 假 | 假 |
一般的,在數學中把用語言、符號或式子表達的,可以判斷真假的陳述句叫做命題。其中判斷為真的語句叫做真命題,判斷為假的語句叫做假命題。等值命題(equivalent propositions),亦稱等價命題或等效命題,是一類...
資金等值計算公式和複利計算公式的形式是相同的。概念定義 設A、B為兩命題公式,若等 價式A B是重言式,則稱A與B是等值的,記作AB.注意,定義中引進的符號“"與“=”或“”混為一談。另外,不難看出命題公式之間的等值關係是...
1個命題變項的取值一般從00...0到1...1或者從1...1到00...0。定義2 設A、B是命題公式,是出現在A和B中的所有命題變項,如果對於 的任何一組賦值,A的真值和B的真值都相同,則稱公式A等值於公式B(或A與B等值),記作A...
∵AB∴A和B具有相同的真值,即A雙條件B永為真,即(A→B)∧(B→A) 。A等價於B就能直接得出A雙條件B。就好比A→B非A∨B一樣,可以用真值表證明 符號 ⇔不是聯結符,它是用來說明A與B等值(A↔B為重言式)的一種記法...
命題連線詞是由命題構成複合命題時所用的邏輯詞。複合命題的真假值由構成它的支命題的真假值確定。最常用的命題連線詞有否定詞、合取詞、析取詞、蘊涵詞、等值詞等。命題連線詞(propositional connectives),也稱作語句連線詞(sentential ...
(4)→:蘊涵詞,A→B讀為“若A則B”,若且唯若命題A是真命題,並且命題B是假命題時,A→B才是假命題。在命題A→B中,A稱為前件,B稱為後件.(5)~:等值詞,A~B讀為“A等值於B”,或“A和B等值”,若且唯若命題A...
條件定義是定義項為條件命題(即假言命題)的定義。如“x是偶數,若且唯若X是整數,則X能為2所整除”。條件定義的定義項與被定義項都表現為等值命題。關係定義是屬加種差定義的一種。用揭示被定義概念所反映的事物間關係作為種差而...
biconditional proposition 等值命題 ; 雙條件命題 ; 詳細翻譯 biconditional gate 雙條件閘 ; 同門 ; [計] 雙條件門 Biconditional Statement 雙條件敘述 ; 雙態語句 ; [計] 雙條件語句 ; 雙向條件述辭 biconditional operation 雙條件...
等價詞(equivalence),亦稱等值詞、雙條件詞,是真值聯結詞之一。通常用“≡”“↔” ,“E”等符號來表示。如果p,q均為命題,則p≡q(或p↔q,Epq,讀“p若且唯若q”)表示由p和q組成的命題“p若且唯若q”,其直覺含義...
在數學上,證明是在一個特定的公理系統中,根據一定的規則或標準,由公理和定理推導出某些命題的過程。比起證據,數學證明一般依靠演繹推理,而不是依靠自然歸納和經驗性的理據。這樣推導出來的命題也叫做該系統中的定理。數學證明建立在...
第四節 直言命題的直接推理 第五節 直言三段論推理 第六節 文恩圖對三段論推理有效性的判定作用 第四章 命題邏輯(上)——複合命題 基本命題推理 第一節 復事命題概述 第二節 基本複合命題 第三節 一般複合命題 等值命題 第四節...
第四節 複合命題 第五節 負複合命題的等值命題 第六節 推理和複合命題推理 第七節 三段論 第八節 歸納推理和類比推理 第九節 求因果關係的方法 第十節 預設 第十一節 典型的邏輯錯誤 數學部分 第二章 函式 極限 連續 ...
(一)醫學假言命題中的條件 (二)充分條件的醫學假言命題 (三)充分條件的醫學假言推理 (四)必要條件的醫學假言命題 (五)必要條件的醫學假言推理 (六)充分必要條件的醫學假言命題 (七)充分必要條件的醫學假言推理 六、醫學等值命題及其...
第三章 命題及簡單命題 第一節 命題及其分類 第二節 直言命題 第三節 關係命題 第四節 規範模態命題 第四章 複合命題 第一節 聯言命題 第二節 選言命題 第三節 假言命題 第四節 負命題及等值命題 第五章 法律形式...
二、選言命題的真值 三、選言命題的套用 第三節 假言命題 一、假言命題概述 二、充分條件假言命題 三、必要條件假言命題 四、充分必要條件假言命題 五、假言命題的套用 第四節 負命題 一、負命題概述 二、負性質命題及其等值命題 三...
一 簡單命題和複合命題 二 聯言命題和聯言推理 三 選言命題和選言推理 四 假言命題和假言推理 五 負命題及其等值命題 六 幾種常用的複合命題推理 第五講 “所有的金子都是閃光的”——直言命題及其推理 ...
相互競爭的結論組成了一個集合,這些結論都是全稱蘊涵命題或全稱等值命題。假定構成這些命題的屬性來自同一個論域,對應於屬性的論域有一個事物的論域。事物論域中的每一個元素對於任意一個結論,或者提供一個確定的例證,或者提供一個...
析取詞是數學邏輯中一種命題連線詞。用符號“∨”表示可兼的(相容的)析取詞,如A∨B即A和B的析取詞,讀作“A或B”,其真假關係是:A和B都假則A∨B假,否則A∨B真。不可兼的(互斥的)析取命題可用等值命題的否定表示,如...
1和0分別解釋為特定的邏輯上真的命題和邏輯上假的命題,或稱有效命題和矛盾命題;=表示兩命題邏輯上等值。這時,填、∨和∧作為命題運算正好滿足形式上與類代數的基本定律相對應的定律,而整個命題代數可包括命題邏輯的全部內容。命題代數...
聯言命題及其推理 歷年真題 基本知識點清單 考點4:選言命題及其推理 歷年真題 基本知識點清單 考點5:假言命題及其推理 歷年真題 基本知識點清單 考點6:負命題及其等值命題 歷年真題 基本知識點清單 考點7:模態命題及其...
2.1.6 等值詞和等值命題 習題2.1 2.2 命題的符號化 2.2.1 什麼是命題的符號化 2.2.2 一些常見的複合命題的符號化 2.2.3 包含多個聯結詞的複合命題的符號化 習題2.2 2.3 命題的真值表及其邏輯性質 2.3.1 真...
一、關係命題 二、關係性質 三、關係三段論 第五章 複合命題推理 第一節 複合命題概述 一、複合命題特徵 二、聯言命題 三、選言命題 四、假言命題 五、等值命題 六、負命題 七、多重複合命題 八、複合命題在法律工作中的套用 第二...
三、等值命題 第二節 直言命題符號化 一、A命題量化 二、E命題量化 三、I命題量化 四、O命題量化 第三節 論證有效性證明 一、歸謬法 二、全稱例示 三、存在例示 四、量化等值 五、證明的一般策略 第四節 直言命題論證有效性證明 ...
會用主析取範式求公式的成真賦值、成假賦值、判斷公式的類型、判斷兩個公式是否等值。析取範式與合取範式 定義2.2 命題變項及其否定統稱作文字。 僅由有限個文字構成的析取式稱為簡單析取式。僅由有限個文字構成的合取式稱為簡單合取...
第2章性質命題與直言三段論 2.1性質命題及其直接推理 2.2直言三段論 第3章複合命題及其推理 3.1聯言命題及其推理 3.2選言命題及其推理 3.3假言命題及其推理 3.4複合命題負命題的等值命題與等值推理 3.5二難推理 3.6命題間的推理...
第2章性質命題與直言三段論 2.1性質命題及其直接推理 2.2直言三段論 第3章複合命題及其推理 3.1聯言命題及其推理 3.2選言命題及其推理 3.3假言命題及其推理 3.4複合命題負命題的等值命題與等值推理 3.5二難推理 3.6命題間的推理...
第2章性質命題與直言三段論 2.1性質命題及其直接推理 2.2直言三段論 第3章複合命題及其推理 3.1聯言命題及其推理 3.2選言命題及其推理 3.3假言命題及其推理 3.4複合命題負命題的等值命題與等值推理 3.5二難推理 3.6命題間的推理...
第2章 性質命題與直言三段論 2.1 性質命題及其直接推理 2.2 直言三段論 第3章 複合命題及其推理 3.1 聯言命題及其推理 3.2 選言命題及其推理 3.3 假言命題及其推理 3.4 複合命題負命題的等值命題與等值推理 3.5 多重複合推理...
