基本介紹
- 中文名:第三類貝塞爾函式
- 外文名:Bessel function of the third kind
- 別稱:漢克爾函式
- 定義:貝塞爾方程的線性無關解
- 一級學科:數學
- 二級學科:特殊函式
歷史
現實背景和套用範圍
第三類貝塞爾函式
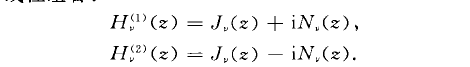 第三類貝塞爾函式
第三類貝塞爾函式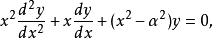
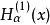
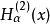
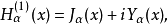
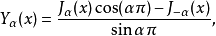
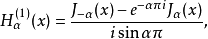
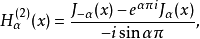
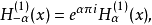
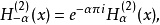
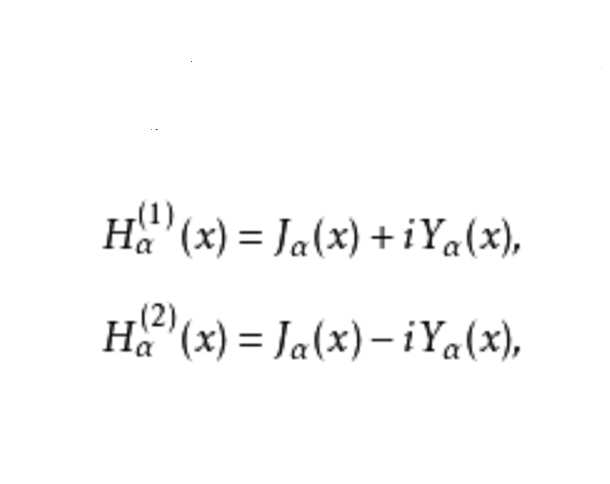
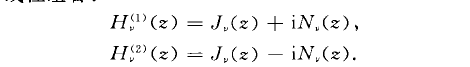 第三類貝塞爾函式
第三類貝塞爾函式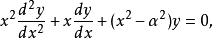
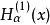
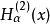
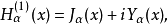
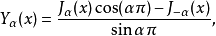
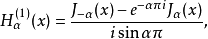
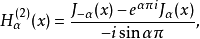
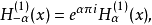
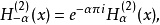
第三類貝塞爾函式(Bessel function of the third kind)亦稱漢克爾函式,貝塞爾方程的線性無關解,可以表示為第一類和第二類貝塞爾函式的線性組合,它們在除去負實軸 (-...
貝塞爾函式是貝塞爾方程的解,它們和其他函式組合成柱調和函式。除初等函式外,在物理和工程中貝塞爾函式是最常用的函式,它們以19世紀德國天文學家F.W.貝塞爾的姓氏...
球貝塞爾函式(spherical Bessel function)球貝塞爾方程的解.即函式jv(x)是v階第一類球貝塞爾函式...
第三類貝塞爾函式(亦稱漢克爾函式)定義為Hn=Jn±iYn,其中i為虛數,用n階( 正或負 )貝塞爾函式可解稱為貝塞爾方程的微分方程。貝塞爾曲線...
5.5.1 貝塞爾函式的零點5.5.2 貝塞爾函式的正交性5.6 貝塞爾函式套用舉例5.7 貝塞爾函式的其他類型5.7.1 第三類貝塞爾函式5.7.2 虛宗量的貝塞爾函式...
安格爾函式是非齊次貝塞爾微分方程的解。貝塞爾函式是貝塞爾方程的解,它們和其他函式組合成柱調和函式。除初等函式外,在物理和工程中貝塞爾函式是最常用的函式,它們以...
5.5.1 貝塞爾函式的零點 5.5.2 貝塞爾函式的正交性 5.6 貝塞爾函式套用舉例 5.7 貝塞爾函式的其他類型 5.7.1 第三類貝塞爾函式 5.7.2 虛宗量的貝...
第二類貝塞爾函式(Bessel function of the second kind ),亦稱諾伊曼函式(Neumann function),為貝塞爾方程的第二解,與第一類貝塞爾函式線性無關,且可由第一類貝塞爾...
本書介紹了物理學科研工作所需的數學知識和相應的數學基礎,包括10章內容,分別是變分法、希爾伯特空間、二階線性常微分方程、貝塞爾函式、狄拉克δ函式、格林函式、...
漢克爾著名的貢獻包括他提出的貝塞爾方程的一類特殊函式解(稱為“第三類貝塞爾函式”或漢克爾函式),和線性代數中的漢克爾矩陣。同時,他還是著名的數學史專家,主要著作...
計算機仿真編程實踐320第17章 貝塞爾函式32117.1 貝塞爾方程及其解32117.1.1 貝塞爾方程32117.1.2 貝塞爾方程的解32117.2 三類貝塞爾函式的表示式及...
4.5.3 連帶勒讓德函式在解數理方程中的套用4.6 球函式4.6.1 一般的球函式定義4.6.2 球函式的正交歸一性4.6.3 球函式的套用4.7貝塞爾函式4.7.1 三類貝塞爾函式...
7.10第三類標準B樣條 330本章小結 338第8章數值微分 3398.1簡單的中點公式...10.6第二類整數階貝塞爾函式 435本章小結 444第11章常微分方程(組)的數值方法...
11.5.5 【實例64】 貝塞爾函式求值 47611.5.6 【實例65】 變型貝塞爾函式...11.6.4 [算法116] 第三類橢圓積分 48611.6.5 【實例66】 第一類勒讓德...
