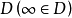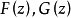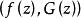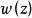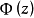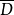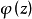對於第一類準解析函式,保持區域定理不一定成立。
設w(z)是區域D內廣義解析函式或第一類準解析函式,則必存在D內解析函式Φ(z)與D上的連續函式φ(z),使得w(z)=Φ(z)eφ(z),這個定理稱為相似原理。
基本介紹
- 中文名:第一類準解析函式
- 外文名:the first kind of pseudoanalytic function
- 適用範圍:數理科學
廣義解析函式,簡介,判定,相似原理,
廣義解析函式
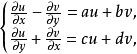

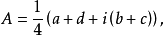
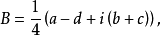
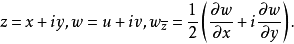
簡介

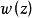

判定
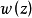
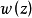

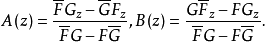
相似原理
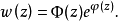
有了相似原理,使得關於解析函式的許多性質,可轉移到廣義解析函式上來,如積分和級數理論、孤立奇點的分類、惟一開拓性、函式序列的凝聚原理及龍格逼近定理等。