球坐標系是三維坐標系的一種,用以確定三維空間中點、線、面以及體的位置,它以坐標原點為參考點,由方位角、仰角和距離構成。球坐標系在地理學、天文學中都有著廣泛套用。
基本介紹
- 中文名:球坐標系
- 外文名:Spherical Coordinates
- 類別:三維坐標系
- 作用:確定三維空間中點線面及體的位置
- 參考點:坐標原點
- 構成要素:方位角、仰角和距離
- 套用領域:數學、物理學、地理學、天文學等
定義,例解,轉換,微分關係,套用,
定義
在數學裡,球坐標系(英語:Spherical coordinate system)是一種利用球坐標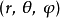 表示一個點 p 在三維空間的位置的三維正交坐標系。右圖顯示了球坐標的幾何意義:原點到 P 點的距離 r ,原點到點 P 的連線與正 z-軸之間的天頂角
表示一個點 p 在三維空間的位置的三維正交坐標系。右圖顯示了球坐標的幾何意義:原點到 P 點的距離 r ,原點到點 P 的連線與正 z-軸之間的天頂角 以及原點到點 P 的連線,在 xy-平面的投影線,與正 x-軸之間的方位角
以及原點到點 P 的連線,在 xy-平面的投影線,與正 x-軸之間的方位角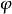 。
。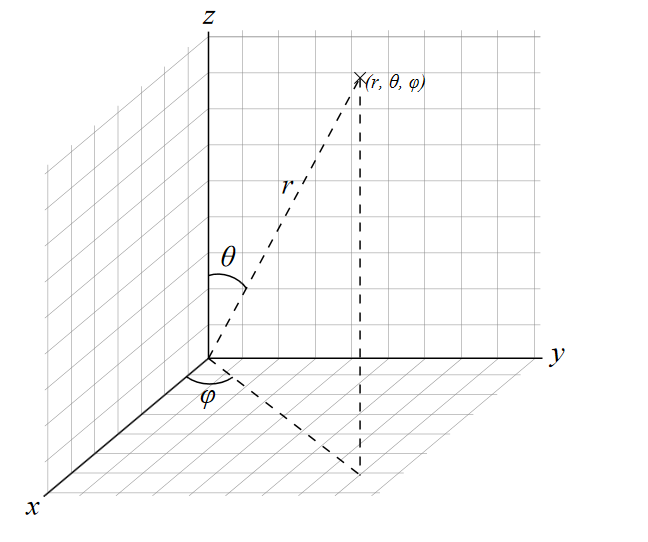 圖1:平面坐標系
圖1:平面坐標系
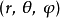

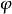
 圖1:平面坐標系
圖1:平面坐標系例解
假設P(x,y,z)為空間內一點,則點P也可用這樣三個有次序的數(r,θ,φ)來確定,其中r為原點O與點P間的距離;θ為有向線段OP與z軸正向的夾角;φ為從正z軸來看自x軸按逆時針方向轉到OM所轉過的角,這裡M為點P在xOy面上的投影;。這樣的三個數r,θ,φ叫做點P的球面坐標,顯然,這裡r,θ,φ的變化範圍為r∈[0,+∞),θ∈[0, π], φ∈[0,2π] ,如圖1所示。
轉換
1).球坐標系(r,θ,φ)與直角坐標系(x,y,z)的轉換關係:
x=rsinθcosφ.
y=rsinθsinφ.
z=rcosθ.
2).反之,直角坐標系(x,y,z)與球坐標系(r,θ,φ)的轉換關係為:


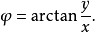
微分關係
在球坐標系中,沿基矢方向的三個線段元為:
dl(r)=dr, dl(φ)=rsinθdφ, dl(θ)=rdθ.
球坐標的面元面積是:
dS=dl(θ)* dl(φ)=r2sinθdθdφ.
體積元的體積為:
dV=dl(r)*dl(θ)*dl(φ)=r2sinθdrdθdφ.
套用
地理坐標系用兩個角值,緯度與經度,來表示地球表面的地點。正如二維直角坐標系專精在平面上,二維球坐標系可以很簡易的設定圓球表面上的點的位置。在這裡,我們認定這圓球是個單位圓球;其半徑是1。通常我們可以忽略這圓球的半徑。在解析旋轉矩陣問題上,這方法是非常有用的。
球坐標系適用於分析一個對稱於點的系統。舉例而言,一個圓球,其直角坐標方程式為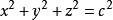 ,可以簡易的用球坐標系
,可以簡易的用球坐標系 來表示。
來表示。
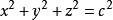

當求解三重積分時,如果定義域為圓球,則面積元素是
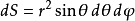
體積元素是

用來描述與分析擁有球狀對稱性質的物理問題,最自然的坐標系,莫非是球坐標系。例如,一個具有質量或電荷的圓球形位勢場。兩種重要的偏微分方程式,拉普拉斯方程與亥姆霍茲方程,在球坐標里,都可以成功的使用分離變數法求得解答。這種方程式在角部分的解答,皆呈球諧函式的形式。
球坐標的概念,延伸至高維空間,則稱為超球坐標(n-sphere)。