稠密環

稠密環(dense ring)是一類特殊環。它是除環上右向量空間的全線性變換環的一個子環，在雅各布森拓撲下，它的閉集等於全線性變換環。

對並與差運算封閉的集類，測度論中重要概念之一。設F是Ω上的一個非空集類.如果它對集的並及差運算封閉，即對任何A，B∈F，都有A∪B∈F，A\B∈F，則稱F為Ω上的環。

基本介紹

• 中文名：稠密環
• 外文名：dense ring
• 領域：數學
• 學科：測度論
• 性質 ：一類特殊的環
• 全稱：稠密線性變換環

概念

稠密環(dense ring)是一類特殊環。它是除環上右向量空間的全線性變換環的一個子環，在雅各布森拓撲下，它的閉集等於全線性變換環。其代數定義是：設R是除環D上向量空間V的全線性變換環的一個子環，若對任意自然數n，V中任意D無關向量x₁，x₂，…，x_n及任意n個向量y₁，y₂，…，y_n，恆有a∈R使得x_ia=y_i，i=1，2，…，n，則R稱為V的稠密線性變換環，簡稱稠密環。當V是D上有限維向量空間時，V僅有惟一的稠密環，即V的全線性變換環。

環

對並與差運算封閉的集類，測度論中重要概念之一。設F是Ω上的一個非空集類.如果它對集的並及差運算封閉，即對任何A，B∈F，都有A∪B∈F，A\B∈F，則稱F為Ω上的環。例如，若F是由實直線R上任意有限個左開右閉的有限區間的並集：

的全體構成的集類，則F是R上的一個環。環也是對於交與對稱差運算封閉的集類，並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上，就需要做一系列奠基工作，其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。

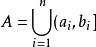
除環

在抽象代數中，除環是一個非零環，其中每個非零元素a都具有乘法逆，即具有x·a=a·x的元素x。換句話說，一個環若且唯若單位組等於所有非零元素的集合的時候它是一個除環。 除環是一種不可交換的環。

除環不同於域，只是因為它們的乘法不需要交換。 然而，通過韋德伯恩的小定理，所有有限除環都是可交換的，因此是有限域。 歷史上，除環有時被稱為域，而域稱為“交換域”。

除了零理想和本身之外，所有除環都是簡單的，即沒有雙面理想。

除環不同於域，只是因為它們的乘法不需要交換。 然而，通過韋德伯恩的小定理，所有有限除環都是可交換的，因此是有限域。 歷史上，除環有時被稱為域，而域稱為“交換域”。

除了零理想和本身之外，所有除環都是簡單的，即沒有雙面理想。

除環（division ring），又譯反稱域或體（skew field）、體，是如下定義的一個環：

至少有一個非零元素，這些非零元素稱為單位(Unit)

非零元素都存在逆元素（左逆元素與右逆元素）

它和域（field）的區別在於除環不必要符合交換律。所有域都是除環。不符合交換律的除環(斜體），例子有四元數體。

向量空間

向量空間又稱線性空間，是線性代數的中心內容和基本概念之一。在解析幾何里引入向量概念後，使許多問題的處理變得更為簡潔和清晰，在此基礎上的進一步抽象化，形成了與域相聯繫的向量空間概念。譬如，實係數多項式的集合在定義適當的運算後構成向量空間，在代數上處理是方便的。單變元實函式的集合在定義適當的運算後，也構成向量空間，研究此類函式向量空間的數學分支稱為泛函分析。

向量空間它的理論和方法在科學技術的各個領域都有廣泛的套用。

線性空間是在考察了大量的數學對象(如幾何學與物理學中的向量，代數學中的n元向量、矩陣、多項式，分析學中的函式等)的本質屬性後抽象出來的數學概念，近代數學中不少的研究對象，如賦范線性空間、模等都與線性空間有著密切的關係。它的理論與方法已經滲透到自然科學、工程技術的許多領域。哈密頓(Hamilton，W.R.)首先引進向量一詞，並開創了向量理論和向量計算。格拉斯曼(Grassmann，H.G.)最早提出多維歐幾里得空間的系統理論。1844—1847年，他與柯西(Cauchy，A.-L.)分別提出了脫離一切空間直觀的、成為一個純粹數學概念的、抽象的n維空間。特普利茨(Toeplitz，O.)將線性代數的主要定理推廣到任意域上的一般的線性空間中。

測度論

亦稱抽象測度論或抽象積分論，研究一般集合上的測度和積分的理論，是勒貝格測度和勒貝格積分理論的進一步抽象和發展。

測度是集合的一種度量，它是長度、面積、體積概念的推廣.首先試圖把長度、面積、體積概念推廣到任意點集而得出一般的“測度”觀念的是杜·布瓦-雷蒙( Du Bois-Reymond，P.D.G.)，他在《一般函式論》(1882年)中提出容量概念，即測度概念的雛形。隨後漢克爾(Hankel，H.)、施托爾茨(Stolz，O.)、哈納克(Harnack，C.G.A.)、康托爾(Cantor，G.(F.P.))等人發展了這種思想。

一般集合上的測度和積分理論是最廣泛的測度理論，但為適應各方面的需要，還出現了其他種種特殊的測度和積分。例如，20世紀30年代初，伴隨著人們對取值於巴拿赫空間的函式性質特別是可微性和可積性的研究，出現了有關向量值測度的一些工作。1960年以後，向量值測度理論得到蓬勃發展，並逐漸趨於完善。又如，19世紀建立的傅立葉分析理論，對於套用數學而言，當時已是令人滿意的數學工具，但由於黎曼積分的局限性，對於函式與展開式之間的關係，直到勒貝格積分理論確立之後才有深刻的揭示。勒貝格積分的出現對於傅立葉展開的研究顯然促進了一大步，但依舊顯示出了它的局限性。研究拓撲群上的測度是建立群上傅立葉分析的基本問題之一，這個問題自1930年以來，經過哈爾(Haar，A.)、韋伊(Weil，A.)和蓋爾范德(Гельфанд，И.М.)等人的工作而趨於完善。再如，20世紀初測度論的建立，使得人們對R中的子集關於n維勒貝格測度的性質有了很好的了解。但在處理與R中低維點集有關的數學問題時遇到了困難。在這種背景下，20世紀20年代出現了幾何測度論，它是研究高維空間中低維點集的測度及低維點集上積分的理論。