相關相似性(Correlation)方法依據雙方共同評分的項目進行用戶相似評價,能夠更好地體現用戶的相似程度,但相關相似性在計算用戶之間相似性上還存在著一些問題。
基本介紹
- 中文名:相關相似性
- 外文名:Correlation
- 涉及學科:信息科學
- 套用:自動化
- 優點:更好地體現用戶的相似程度
簡介
相似性度量
相似性度量方法
餘弦相似性

修正餘弦相似性

相關相似性

相關相似性缺點
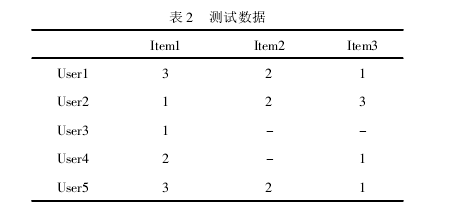
相似性計算方法
常態分配函式




修正函式







改進後的相似性計算方法


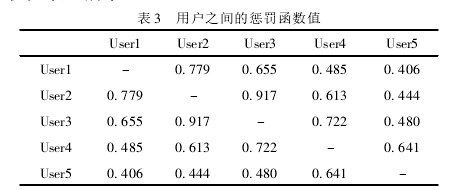
相關相似性(Correlation)方法依據雙方共同評分的項目進行用戶相似評價,能夠更好地體現用戶的相似程度,但相關相似性在計算用戶之間相似性上還存在著一些問題。


















相關相似性(Correlation)方法依據雙方共同評分的項目進行用戶相似評價,能夠更好地體現用戶的相似程度,但相關相似性在計算用戶之間相似性上還存在著一些問題。簡介為了讓用戶從大量信息中找到自己感興趣的信息,推薦系統已...
相似性度量,即綜合評定兩個事物之間相近程度的一種度量。兩個事物越接近,它們的相似性度量也就越大,而兩個事物越疏遠,它們的相似性度量也就越小。相似性度量的給法種類繁多,一般根據實際問題進行選用。常用的相似性度是有:相關...
普遍性 自然界的相似性 在自然界中,大至宇宙星系之間,小至每個原子運動的形式,都存在著大量的相似之處。自然界的相似性 先看看宇宙星系。學過地理的人都知道,月球圍著地球轉,地球圍著太陽轉。當我們的目光遠離地球,鎖定茫茫的太陽...
比較分子相似性指數分析(COMSIA)用來計算分子周圍格線交叉點上的相似性指數。採用偏最小二乘回歸分析(PLS)建立雌激素類化合物活性與結構之間的定量關係,以“逐一剔除”(LOO)和SAMPLS程式確定最佳主成分數PCs,然後再計算非交叉驗證相關...
相關係數(correlation coefficient)是一個數,它表示兩個等長度信號之間的相似性。例如,在時序n=a~b的兩個數位訊號x(n)和y(n),其相關係數寫為 式中a和b都是整數,符號“*”表示複數共軛,相關係數的絕對值|r|≤1。當|r|=1...
相關函式是描述信號X(s),Y(t)(這兩個信號可以是隨機的,也可以是確定的)在任意兩個不同時刻s、t的取值之間的相關程度。定義 相關函式 相關函式描述了兩個信號之間的相似性,其相關性大小有相關係數衡量。相關係數 定義 稱為變數X...
在自然科學領域中,皮爾遜相關係數廣泛用於度量兩個變數之間的相關程度,其值介於-1與1之間。它是由卡爾·皮爾遜從弗朗西斯·高爾頓在19世紀80年代提出的一個相似卻又稍有不同的想法演變而來的。這個相關係數也稱作“皮爾遜積矩相關係數”...
《河網形態的自相似性及其相關問題研究》是依託中南大學,由戴斌祥擔任項目負責人的專項基金項目。項目摘要 河網拓撲結構反映地表水系的形態結構特徵,是河床演變、數字流域以及河流地貌研究的基礎問題。針對由Tokunaga自相似網路所生成的河網難以...
從物理上看,互相關運算的結果反映了兩個信號之間相似性的量度。特別是對於實函式f(x)和h(x)而言,其相關運算相當於求兩函式的曲線相對平移 1個參變數x後形成的重疊部分與橫軸所圍區域的面積。定義 兩個函式f(x)和h(x)的互相關...
生理狀態相似性 除了環境方面的背景信息能影響學習者的記憶外,個人方面的背景信息如心境、意識水平甚至生理狀態同樣會影響記憶的效果。我們的情緒興奮時,能回想出許多愉快的事,心境不佳時能回想出許多不愉快的事。我們常常聽人這么說:...
相關多元化是多元化形式和戰略之一。企業經營的多種業務存在某些明顯的實質相似性,即強調多種業務可在很大程度上共享企業的技術、價值鏈活動和企業的其他資源和能力。目的是使企業經營的業務組合產生協同效應。應注意的是,相關性只是產生...
相似變換 基本概念 關於相似群的圖形的不變性質和不變數分別稱為相似性質和相似不變數,如角度等,研究相似性質和相似不變數的幾何稱為相似幾何。關於射影群的圖形的不變性質和不變數分別稱為射影性質和射影不變數,如同素性、結合性、交...
自相似過程的方差要慢於短相關過程。長相關性 若一個隨機過程滿足自相似的條件1和條件2,即其自相關函式滿足隨時滯的增加成雙曲線衰減(冪率衰減),則該隨機過程呈現長相關性。其它特點 一個系統的自相似性是指某種結構或過程的特徵...
模擬相似條件(alalogical conditions of simulation)是指為了使地球物理模擬得到的地球物理場的特徵與野外實際觀測的物理場特徵基本一致,需要滿足這樣的相似條件:模型與原型的邊界、空間條件及幾何尺度具有相似性;模型與原型的時間條件應...
光譜相似尺度 光譜相似尺度是一個物理學名詞。光譜相似尺度是通過同時度量兩個光譜之間的大小和形狀來判定光譜相似性的,而傳統的光譜相似性度量方法(如:歐氏距離、相關係數、光譜角等)只計算兩個光譜之間的大小(亮度)或形狀 ...
與Jaccard 係數相關的指標叫做Jaccard 距離,用於描述集合之間的不相似度。Jaccard 距離越大,樣本相似度越低。公式定義如下:其中對稱差(symmetric difference) 。性質 相似性 非對稱二元屬性的相似性 在數據挖掘領域,常常需要比較兩個...
為解決傳統層次分析法在權重分配過程中主觀性過強的缺陷,夏春艷等改進層次分析法,提出基於信度係數的人機界面評價指標權重分配方法根據人類思維具有模糊性和灰色性的特點,將灰色關聯分析引入到層次分析法中,從整體相似性的角度構造專家判斷...
化學結構相似性 具有相同的官能團,如醛基 、 環氧化物 、 酉旨鍵 、 特殊的金屬離子等; 規律性變化,如碳鏈的依次增加或縮短等,主要是一 些碳氫化合物的溶劑 、 石油產物 、 天然複合物; 額外增加或缺失官能團不會影響物質最終...
