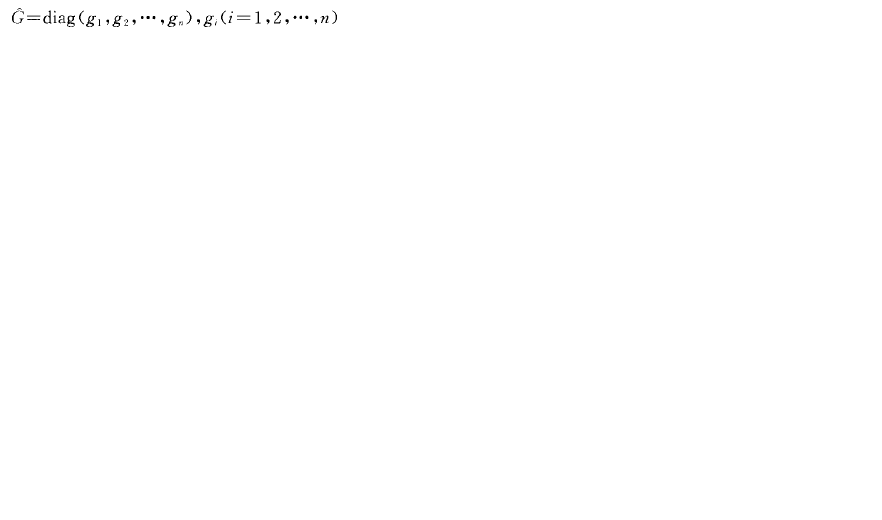
直接投入係數矩陣（direct input coefficient matrix）亦稱投入係數矩陣。U表的一種無量綱係數矩陣，是指產品（行）×產業部門（列）的係數矩陣，用B表示。
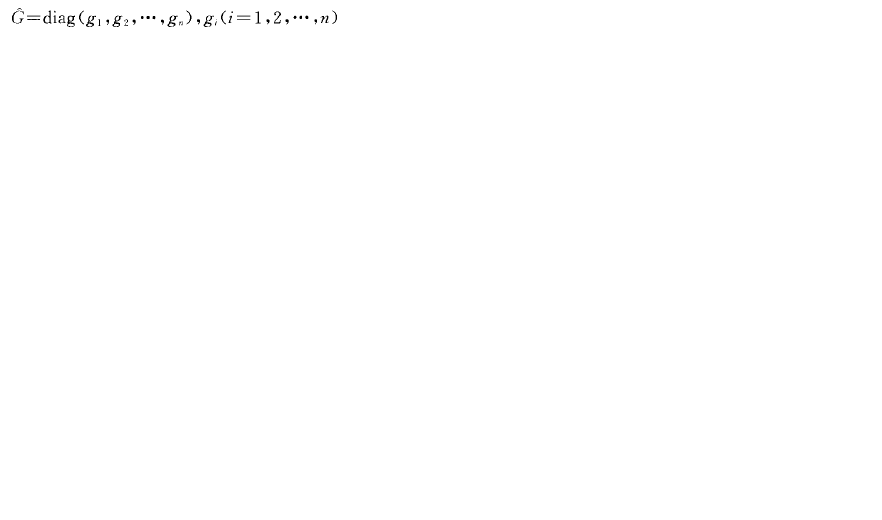
直接投入係數矩陣（direct input coefficient matrix）亦稱投入係數矩陣。U表的一種無量綱係數矩陣，是指產品（行）×產業部門（列）的係數矩陣，用B表示。計算公式式中U是產品對產業部門的投入矩陣（...
第j部門生產單位產品直接消耗第i部門的產品量，稱為第j部門對第i部門的直接消耗係數，以aij表示（其中"i"、"j"為下標，以下類同）．即 aij=xij/xj (i,j=1,2,3,…,n)各部門之間的直接消耗係數構成的n階矩陣 a11 a12 .....
公式矩陣 將各產品部門的需要消耗係數用表的形式表現出來，就是需要消耗係數表或完全消耗係數矩陣，通常用字母B表示。需要消耗係數的計算公式為:式中的第一項aij表示第j產品部門對第i產品部門的直接消耗量；式中的第二項表示第j產品部門...
在投入產出表的基礎上，可以建立以下投入產出模型 產品平衡模型 A x + y = x ，式中A是直接消耗係數矩陣；x 為各部門總產值列向量；y 為最終產品列向量。移項求逆後得：（I-A）-1y=x， 式中I為單位矩陣。 價值構成...
式中A={aij}和B={bij}分別表示直接消耗係數矩陣和完全消耗係數矩陣。因矩陣A的最大特徵根之模小於1，因此A和B有如下關係：B=（I－A）－I 動態投入產出模型 靜態投入產出模型主要用來說明本時期的生產和消耗部門間的平衡關係和...
因此，可以把灰色系統理論的方法與投入產出模型結合起來，研究灰色投人產出問題。定義1 設 為 部門消耗 部門產品的價值總量，稱 為流量矩陣。定義2 設 為 部門消耗 部門產品的價值總量，為 部門的總產出，稱 為直接消耗係數。直接消耗...
，W≥0的約束條件下，使Z‘=WR達到最小值。以上各式中：D為生產單位產品的消耗直接消耗係數矩陣；X為總產值向量；R為資源向量；Z、Z‘為目標函式；P為單位產品價格；I為單位矩陣；A為產品直接消耗係數矩陣；W為資源影子價格。
可見，是否合理的選擇基數，對使用係數是有影響的。電路面積最佳化 為縮短布爾函式系統混合極性Reed－Muller（mixed－polarity Reed－Muller，MPRM）電路面積最佳化過程的時間，提出了能在任意極性值的MPRM間進行極性轉換的係數矩陣變換方法。使用...
初等行變換不影響線性方程組的解，也可用於高斯消元法，用於逐漸將係數矩陣化為標準形。初等行變換不改變矩陣的核（故不改變解集），但改變了矩陣的像。反過來，初等列變換沒有改變像卻改變了核。（2）用於求解一個矩陣的逆矩陣 有的...
式中X=＜x,xZ,...,xn`是產品部門總產出列向量，A是n階直接消耗係數矩陣，B是n階投資係數矩陣，S是產品部門最終淨產品列向量，a;，和b;，分別表示兩個產品部門間的直接消耗係數和投資係數.和封閉式投入產出模型比較，方程的右端...
封閉式投入產出模型它是列昂節夫(I,eontief , W.)於1953年提出的這個模型由一個齊次線性常微分方程組描述,其具體形式為 式中X= Cx x2, ''.. xnz’是產品部門總產出列向量,A是n階直接消耗係數矩陣,B是n階投資係數矩陣,a;...
差分方程的動態模型實現了直接消耗係數矩陣和投資係數矩陣的動態化。不僅可以根據經濟問題需要選取時間區間，而且可以考慮投資的時滯等問題。隨後原聯邦德國學者彼得·卡爾門巴克(Peter Kalmbach)和奧地利學者亨茲·D·庫爾茨(Heinz D，Kurz)...
《線性代數（第2版）》是陳殿友、術洪亮編著，2014年4月由清華大學出版社出版的普通高等教育“十一五”國家級規劃教材。該書可作為高等學校經濟、管理、金融及相關專業的教材或教學參考書。全書共6章，主要內容包括：行列式、矩陣、向量組...
三角分解法亦稱因子分解法，由消元法演變而來的解線性方程組的一類方法。設方程組的矩陣形式為Ax=b，三角分解法就是將係數矩陣A分解為一個下三角矩陣L和一個上三角矩陣U之積：A=LU，然後依次解兩個三角形方程組Ly=b和Ux=y，而...
式中 L 代表不同經濟部門所需的勞動力向量，B 代表勞動力利用係數矩陣，I 代表等同於經濟部門相應位置的階的單位矩陣，A 代表投入—產出技術係數矩陣，F 代表目標年的需求向量。利用此式可根據目標年對商品和勞務的需求、技術和勞動...
（1）部門工藝假定：同一產業部門生產的各種產品投入構成相同。（2）產品工藝假定：不論由哪個部門生產，同一種產品的投入構成相同。5.推導公式 （1）按照部門工藝假定，產品×產品投入產出係數矩陣Ad的計算公式 Ad = HD aij ：第j個...
