簡介 投入產出分析,是研究經濟系統各個部分間表現為投入與產出的相互依存關係的經濟數量方法。
(
鐘契夫 ,陳錫康,劉起運,《投入產出分析》,
中國財政經濟出版社 ,1993.pp1)投入是進行一項活動的消耗。如生產過程的消耗包括本系統內各部門產品的消耗(中間投入)和初始投入要素的消耗(最初投入)。產出是指進行一項活動的結果。如生產活動的結果是為本系統各部分生產的產品(物質產品和勞務)。(陳錫康,投入產出分析講義,2004)
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入產出賬戶的創始人(SURVEY OF CURRENT BUSINESS,March 1999,pp9)。1936年,列昂剔夫發表了《美國經濟體系中的投入產出的數量關係》一文,接著在1941年又出版了《美國經濟結構1919—1929》一書,1953年,又出版了《美國經濟結構研究》一書。在這些著作中,列昂剔夫提出了投入產出方法。(
何其祥 ,《投入產出分析》,科學出版社,1999.pp4)
列昂剔夫的投入產出思想的淵源可以追溯到重農學派魁奈(Francois Quesnay,1694—1774年)著名的《經濟表》。列昂剔夫把他編的第一張投入產出表稱為“美國的經濟表”。數理經濟學派瓦爾拉(Walras,1834—1910)和
帕累托 (Vilfredo Pareto,1848—1923)的
一般均衡理論 和
數學方法 在經濟學中的套用構成了列昂剔夫體系的基礎。(瓦西里·列昂剔夫,《
投入產出經濟學 》(譯序),
商務印書館 ,1980.ppii)列昂剔夫本人認為“投入產出分析是全部相互依存這一古典經濟理論的具體延伸”。
理論基礎 是L.瓦爾拉斯的一般均衡論。在中國,對投入產出分析從經濟理論上進行改造後,通常稱為投入產出原理,它的理論基礎包括勞動價值論、生產資料生產與消費資料生產兩大部類的理論等等。
投入產出表 投入產出分析是通過編制投入產出表來實現的。投入產出表有實物和價值兩種形式:
實物表 亦稱綜合物資平衡表,按實物單位計量,主欄為各種產品,賓欄有三部分:①“資源”。反映各種產品的來源,如年初庫存(或儲備)、當年生產、進口和其他來源。②“中間產品”。這一部分的項數、所列產品名稱、排列都和主欄相同順序,形成一個
棋盤式平衡表 。③“最終產品”。分別列出
固定資產 的更新、改造、大修,年末庫存(或儲備),集體消費,個人消費和出口。這種平衡表的另一種形式,是去掉“資源”部分,將它與“最終產品”部分的有關項目合併,如將年初庫存(或儲備)與年末庫存(或儲備)合併成為庫存(或儲備)變化差額,將進口與出口合併成為進出口差額,列入“最終產品”部分。
價值表 按純部分編制的。純部分是由生產工藝、消耗構成、產品用途基本相同的產品所構成的部門。 投入產出分析
表可以從橫向和縱列兩個方向進行考察,橫向從
使用價值 的角度反映各部門產品的分配使用情況,分為第一、第二兩部分;縱列反映部門產品的價值形成,分為第一、第三部分。第四部分反映非生產部門和個人通過
國民收入再分配 所得到的收入,一般不編這一部分。
數學模型 在投入產出表的基礎上,可以建立以下投入產出模型
投入產出分析 移項 求逆後得:(
I -
A )-1y=x, 式中I為
單位矩陣 。 價值構成模型 ATx+v+m =x,式中,AT為A的
轉置矩陣 ;v為勞動報酬;m 為剩餘產品。 移項求逆後得:(I-AT)-1(v+m )=x。 消耗
係數 在投入產出原理中,消耗係數分為
直接消耗係數 和完全消耗係數。前者又稱為投入係數、工藝係數或技術係數,用於反映國民經濟的生產技術結構,一般用符號a ij表示,即純部門j生產單位產品對純部門i產品的
消耗量 ,如煉一噸鋼所消耗的生鐵。計算公式是 式中
x ij 為
j 部門生產產品時對
i 部門產品的消耗量,又叫做中間流量;
x j 為
j 部門的產量。
直接消耗係數與計畫統計工作中廣泛使用的消耗定額基本相同,但也有一些區別。其區別表現在:①消耗定額是指生產單位產品的工藝消耗量,直接消耗係數除這種消耗外,還包括車間、厂部和公司的相應消耗;②消耗定額一般只按實物計量,而直接消耗係數除按實物計量外,還採用貨幣計量;③消耗定額一般是按某種產品的具體品種、型號確定的,如鋼材的具體品種、型號,而直接消耗係數一般是按大類產品(如鋼材)確定的。
在
直接消耗係數 的基礎上可以計算出完全消耗係數,它是生產單位最終產品對某種總產品或中間產品的直接消耗與間接消耗之和。例如,生產一台機器除直接消耗鋼材外,還要消耗電力,而發電需要設備,生產設備又要消耗鋼材。生產機器通過電力發電設備對鋼材的消耗,叫做間接消耗。
生產單位
k 種最終產品對
i 種產品的完全消耗係數(記作
b ik )的計算公式是 (i,j,k=1,2,3,…,n)
計算公式 上式寫成矩陣為B =A B +I 。由此得
B=(I-A)-1
完全消耗係數還有另一種計算公式(
i ,
j ,
k =1,2,3,…,
n )
計算公式 式中c ik 為生產單位k 種最終產品對i 種產品的完全消耗係數。上式寫成矩陣為C =A +A C 。由此得:
C=(I-A)-1A
兩種完全消耗係數的關係如下:
B-C=(I-A)-1-(I-A)-1A=(I-A)-1(I-A)=I
由此可見,兩種完全消耗係數的區別是一個單位矩陣,它的主對角線上的元素為1,其他元素為0。從經濟含義上講,最終產品是脫離生產過程的產品,不應包含在生產消耗中,應以係數C 作為完全消耗係數,但係數B 是計算C 的基礎,並可以反映最終產品與總產品之間的依存關係。
實際套用 上面所說的是
靜態投入產出模型 ,利用它可以進行經濟分析、政策模擬、計畫論證和
經濟預測 ,並為電子計算機在經濟管理中的套用開闢了途徑。
投入產出分析的提出已經近半個世紀,在這段時間裡,它有很大的發展。除上面所說的產品模型外,還有
固定資產 模型、生產能力模型、投資模型、勞動模型以及研究人口、環境保護等專門問題的模型。除上面所說的
靜態模型 外,還有動態模型、最佳化模型等。
 投入產出分析
投入產出分析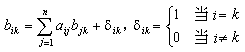 計算公式
計算公式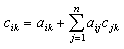 計算公式
計算公式