皮爾遜分布族

皮爾遜分布族簡稱皮爾遜(Pearson)分布， 又稱“皮爾遜曲線族”，是一種常見連續型分布族，是在1895年左右由英國統計學家卡爾·皮爾遜提出的一組頻率分布，其中第Ⅲ型頻率分布常用於水文計算。皮爾遜引進的一個包含四個參數的分布族。它的機率密度函式p(x)由下列微分方程確定：dp(x)/dx=[(x-a)/(b₂x²+b₁x+b₀)]p(x)。一旦有了數據，就用適當方法從皮爾遜曲線族中挑選一條曲線去擬合數據所屬的總體分布。皮爾遜曲線族很大，可分為十二種類型。既包括常用的常態分配，還包括在實際中有廣泛套用的偏態分布。如：一型分布是B分布，二型分布曲線是對稱的U形曲線、三型是移位Γ分布，五型是移位逆Γ分布，六型是逆B分布，七型是t分布，八型是冪函式分布，十型是指數分布，十一型是常態分配……，曲線族的出現，打破了“常態分配是全能的”傳統觀念，在數理統計發展史上是一個重大突破。

基本介紹

• 中文名：皮爾遜分布族
• 外文名：Pearson distributions 
• 別稱：皮爾遜曲線族、皮爾遜分布
• 所屬學科：數學
• 所屬問題：統計學（機率分布）
• 屬性：一種常見連續型分布族
• 簡介：皮爾遜曲線族可分為十二種類型

基本介紹

皮爾遜分布族簡稱皮爾遜分布，是一種常見連續型分布族，其機率密度f(x)決定於微分方程

其中分布參數a₀，b₀，b₁，b₂當a₁=1時完全決定於分布的前四階中心矩μ₂=σ，μ₃和μ₄或矩比：

其中

密度函式f(x)的通解為

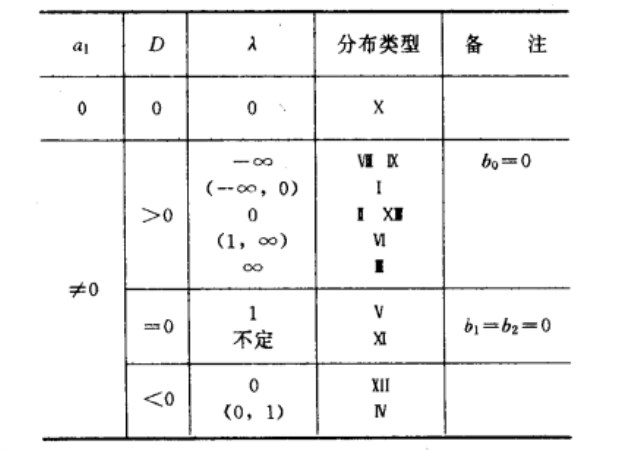
皮爾遜分布族的分類

按二次方程b₀+b₁x+b₂x=0的根的不同分布，區分12種類型的皮爾遜分布。設，則根據D，λ可以判斷皮爾遜分布的類型：

表1 皮爾遜分布的類型

a1	D	λ	分布類型	備 注
0	0	0	Ⅹ
≠0	>0	-∞(-∞，0); 0; (1，∞); ∞	Ⅶ ⅨⅠ; Ⅱ ⅩⅢ; Ⅵ; Ⅲ	b0=0
	=0	1不定	ⅤⅪ	b1=b2=0
	<0	0(0，1)	ⅫⅣ

亦可根據矩比β₁和β₂判斷皮爾遜分布的類型。為此，首先計算

然後按下表作出判斷：

表2皮爾遜分布的類型

F值		(-∞，0)	0			(0，1)	1	(1，∞)	∞
矩比	β1		0	0	0
	β2		<3	=3	>3
分布類型		Ⅰ	Ⅱ	Ⅺ	Ⅻ	Ⅳ	Ⅴ	Ⅵ	Ⅲ

如，一型分布是B分布，二型分布曲線是對稱的U形曲線、三型是移位Γ分布，五型是移位逆Γ分布，六型是逆B分布，七型是t分布，八型是冪函式分布，十型是指數分布，十一型是常態分配……

皮爾遜分布用於統計數據之經驗分布的修勻或理論分布的選配。為此，首先將係數b₀，b₁和b₂中的中心矩μ₂，μ₃和μ₄用相應的樣本中心矩代替，並將所得估計值和代入密度f(x)的方程，其解即統計數據的修勻密度。