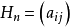基本介紹
簡介,求解方法,判定方法,
簡介
病態矩陣是一種特殊矩陣。指條件數很大的非奇異矩陣。病態矩陣的逆和以其為係數矩陣的方程組的界對微小擾動十分敏感,對數值求解會帶來很大困難。
求解方法
求解方程組時對數據的小擾動很敏感的矩陣。
解線性方程組Ax=b時,若對於係數矩陣A及右端項b的小擾動 δA、δb,方程組 (A+δA)χ=b+δb的解 χ 與原方程組Ax=b的解差別很大,則稱矩陣A為病態矩陣。方程組的近似解 χ 一般都不可能恰好使剩餘 r=b-Aχ 為零,這時 χ 亦可看作小擾動問題Aχ=b-r(即δA=0,δb=-r) 的解,所以當A為病態時,即使剩餘很小,仍可能得到一個與真解相差很大的近似解。
判定方法
判定矩陣是否病態以及衡量矩陣的病態程度通常是看矩陣A的條件數K(A)=‖A-1‖*‖A‖ 的大小,其中 A-1 為矩陣 A 的逆, ‖‖ 表示對矩陣取某一種範數。 K(A) 稱為 A 的條件數,它很大時,稱 A 為病態,否則稱良態; K(A) 愈大, A 的病態程度就愈嚴重。
對小擾動問題 (A+δA)χ=b+δb 與原問題 Ax=b 的解有估計式

對矩陣求逆亦有估計式 從上估計式可以看出條件數對解方程組及矩陣求逆的影響。
從上估計式可以看出條件數對解方程組及矩陣求逆的影響。

由於Hn對稱正定,當取 ‖Hn‖ 為歐氏範數時,K(Hn) 即為Hn 的最大與最小特徵值之比。對n=7,8,9,10有K(H7)=4.75×108,K(H8)=1.53×1010,K(H9)=4.93×1011,K(H10)=1.60×1013。