推理依據,假設檢驗,牛頓的猜想,猜想的依據,檢驗的思想,檢驗的結果,萬有引力,公式表示,適用範圍,引力常量,科學意義,力學套用,自由落體運動,重力與引力,勻速圓周運動,天體力學領域,存在問題,理論問題,觀測問題,理論局限性,演化過程,過往理論,牛頓的萬有引力定律,廣義相對論,參考文獻,
推理依據 伽利略 在1632年實際上已經提出
離心力 和
向心力 的初步想法。布里阿德在1645年提出了引力平方比關係的思想.牛頓在1665~1666年的手稿中,用自己的方式證明了離心力定律,但向心力這個詞可能首先出現在《
論運動 》的第一個手稿中。一般人認為離心力定律是
惠更斯 在1673年發表的《
擺鐘 》一書中提出來的。根據1684年8月~10月的《論迴轉物體的運動》一文手稿中,牛頓很可能在這個手稿中第一次提出向心力及其定義。
萬有引力與相作用的物體的質量乘積成正比,是發現引力平方反比定律過渡到發現萬有引力定律的必要階段.·牛頓從1665年至1685年,花了整整20年的時間,才沿著離心力—向心力—重力—萬有引力概念的演化順序,終於提出“
萬有引力 ”這個概念和辭彙。·牛頓在《
自然哲學的數學原理 》第三卷中寫道:“最後,如果由實驗和天文學觀測,普遍顯示出地球周圍的一切天體被地球重力所吸引,並且其重力與它們各自含有的物質之量成比例,則月球同樣按照物質之量被地球重力所吸引。另一方面,它顯示出,我們的海洋被月球重力所吸引;並且一切行星相互被重力所吸引,
彗星 同樣被太陽的重力所吸引。由於這個規則,我們必須普遍承認,一切物體,不論是什麼,都被賦與了相互的引力(gravitation)的原理。因為根據這個表象所得出的一切物體的
萬有引力 (universal gravitation)的論證……”
牛頓 在1665~1666年間只用離心力定律和
克卜勒第三定律 ,因而只能證明
圓軌道 上的而不是
橢圓軌道 上的引力平方反比關係。在1679年,他知道運用克卜勒第二定律,但是在證明方法上沒有突破,仍停留在1665~1666年的水平。只是到了1684年1月,
哈雷 、
雷恩 、
胡克 和牛頓都能夠證明圓軌道上的引力平方反比關係,都已經知道橢圓軌道上遵守引力平方反比關係,但是最後可能只有牛頓才根據克卜勒第三定律、從離心力定律演化出的向心力定律和數學上的極限概念或
微積分 概念,才用
幾何 法證明了這個難題。
假設檢驗 牛頓的猜想 地球與太陽之間的吸引力與地球對周圍物體的引力可能是同一種力,
遵循 相同的規律。
猜想的依據 (1)
行星 與太陽之間的引力使行星不能飛離太陽,物體與地球之間的引力使物體不能離開地球;(2)在離地面很高的距離里,都不會發現
重力 有明顯的減弱,那么這個力必然延伸到很遠的地方。
檢驗的思想 檢驗的結果 地面物體所受地球的引力,與月球所受地球的引力是同一種力。
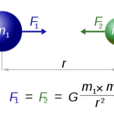
萬有引力 公式表示 F: 兩個物體之間的引力
m1 : 物體1的質量
m2 : 物體2的質量
r: 兩個物體之間的距離(大小)(r 表示徑向矢量)
依照國際單位制,F的單位為
牛頓 (N),m
1 和m
2 的單位為千克(kg),r 的單位為米(m),常數G近似地等於
G=6.67×10- 1 1 N·m2 /kg2 (牛頓平方米每二次方千克)。
由此可知排斥力F一直都將不存在,這意味著淨
加速度 的力是絕對的。(這個符號規約是為了與
庫侖定律 相容而訂立的,在庫侖定律中絕對的力表示兩個
電子 之間的作用力。)
適用範圍 經典萬有引力定律反映了一定歷史階段人類對引力的認識,在十九世紀末發現,
水星 在
近日點 的移動速度比理論值大,即發現水星軌道有旋緊,軌道旋緊的快慢的實際值為每世紀42.9″。這種現象用萬有引力定律無法解釋,而根據
廣義相對論 計算的結果旋緊是每世紀43.0″,在觀測誤差允許的範圍內。此外,廣義相對論還能較好地解釋譜線的
紅移 和光線在
太陽 引力作用下的
偏轉 等現象。這表明廣義相對論的引力理論比經典的引力理論進了一步。
在
法拉第 和
麥克斯韋 之後,人們看到物理的實在除了
粒子 還有電磁場。
電磁場 具有
動量 和
能量 且能傳播
電磁波 。這使人們聯想萬有引力定律也是物理的實在,能傳播引力波,也有許多人努力探測它,但尚無很好的結果。電磁波的傳播可用光子解釋,類似地,光子也導致引力子概念的引出。萬有引力也不再是
超距作用 ,而以
引力子 為媒介。但這些都是物理學家正在探索的領域。
經典力學的適用範圍並引入
普朗克常量 和真空中
光速 來界定
經典力學 的領地。粗糙的說,經典的萬有引力定律適用範圍也可用一數量表示。現在引入引力半徑
,G、m分別表示引力常量和產生引力場的球體的球體的質量,c為光速。用R表示產生力場球體之半徑,若
,則可用牛頓
引力定律 。對於太陽,
,套用牛頓引力定律無問題;即使是對緻密的
白矮星 ,
,也仍然可用牛頓
萬有引力定律 ;至於
黑洞 和
宇宙大爆炸 ,應當是套用
廣義相對論 的。
引力常量 牛頓在推出萬有引力定律時,沒能得出引力常量G的具體值。G的數值於1789年由
卡文迪許 利用他所發明的
扭秤 得出。
卡文迪許 的扭秤試驗,不僅以實踐證明了萬有引力定律,同時也讓此定律有了更廣泛的使用價值。
扭秤的基本原理是在一根剛性桿的兩端連結相距一定高度的兩個相同質量的重物,通過
秤桿 的中心用一扭絲懸掛起來。
秤桿 可以繞扭絲自由轉動,當重力場不均勻時,兩個質量所受的重力不平行。這個方向上的微小差別在兩個質量上引起小的水平
分力 ,並產生一個力矩使懸掛系統繞扭絲轉動,直到與扭絲的扭矩平衡為止。扭絲上的小鏡將光線反射到記錄相板上。當扭絲轉動時,光線在相板上移動的距離標誌著扭轉角的大小。
平衡位置 與扭秤常數和重力位二次導數有關。在一個測點上至少觀測3個方位,確定4個二次導數值,
測量精度 一般達幾
厄缶 。
根據
扭力 系統的構造形狀,分為z型、L型和斜臂式扭秤。z型扭秤由一個輕金屬製成的z型秤臂、兩個質量相等的重荷和一根細金屬絲組成的。兩個重荷分別固定在z型秤臂的兩端。細金屬絲將整個系統懸掛起來,組成一套扭力系統。由於兩個重荷處於不同的位置,所以,當通過兩個重荷的重力等位面Q
1 和Q
2 。互不平行或彎曲時,兩個重荷將受到
重力場 水平分量的作用。當
重力場 水平分量gH
1 和gH
2 的大小和方向不同時,稈臂就要繞著扭絲轉動,直到水平旋轉的重
力矩 和扭絲的
扭力矩 相平衡為止。秤臂偏轉的角度除和扭力系統的構造和扭絲的扭力係數有關外,還和兩個重荷間的重力變化有關。因此,準確記錄扭力系統的偏角,就可以求出重力位的二次導數。由於扭力系統的靈敏度很高,秤臂穩定下來的時間較長。同時還需要在3~5個方向上照相記錄,所以,儀器附有自動控制系統,並安放在特製的小房裡工作。儀器的操作和測量結果的計算都比較煩瑣,每測—個點需要2~3小時,工件效率較低。
扭秤的測量結果用矢量圖表示,用一短線表示曲率,矢量方向相應於最小曲率平面的方位,矢量長度表示等位面曲率差大小 。在短線中心以箭頭畫出總梯度,指向重力增加的方向。
扭秤的靈敏度很高並可測多個參數,但是也有其不足之處。由於具有極高的靈敏度,對於測試環境的要求也很高,易受外界干擾,包括溫度、地面震動、
大氣壓強 波動、扭絲的
滯彈性 效應等。因此對於
精度 要求不高的重力測量工作,一般都是重力儀去完成。但是對於高精度的測量,如
引力 物理方面的測量,以及高精度儀器的驗證以及標定,都需要利用扭秤來完成。因此即便是如今,扭秤在
實驗物理 領域也有著相當重要的地位。
卡文迪許測出的G=6.67×10
- 1 1 N·m
2 /kg
2 ,與現在的公認值6.67×10
- 1 1 N·m
2 /kg
2 極為接近;直到1969年G的測量精度還保持在
卡文迪許 的水平上。
科學意義 萬有引力定律的發現,是17世紀自然科學最偉大的成果之一。它把地面上物體運動的規律和
天體 運動的規律統一了起來,對以後
物理學 和
天文學 的發展具有深遠的影響。它第一次解釋了(自然界中四種相互作用之一)一種
基本相互作用 的規律,在人類認識自然的歷史上樹立了一座里程碑。
萬有引力定律揭示了天體運動的規律,在
天文學 上和宇宙航行計算方面有著廣泛的套用。它為實際的天文觀測提供了一套計算方法,可以只憑少數觀測資料,就能算出長周期運行的天體運動軌道,科學史上
哈雷彗星 、
海王星 、
冥王星 的發現,都是套用萬有引力定律取得重大成就的例子。利用萬有引力公式,
克卜勒 第三定律等還可以計算太陽、地球等無法直接測量的天體的質量。牛頓還解釋了月亮和太陽的萬有引力引起的
潮汐現象 。他依據萬有引力定律和其他
力學 定律,對地球兩極呈扁平形狀的原因和地軸複雜的運動,也成功的做了說明。推翻了古代人類認為的神之引力。
對文化發展有重大意義:使人們建立了有能力理解天地間的各種事物的信心,解放了人們的思想,在科學文化的發展史上起了積極的推動作用。
力學套用 自由落體運動 同理亦可得出a2 .
請注意上述方程中的a
1 ,質量m
1 的
加速度 ,在實際上並不取決於m
1 的取值。因此可推論出對於任何物體,無論它們的質量為多少,它們都將按照同樣的比率向地面墜落(忽略空氣阻力)。
如果物體運動過程中r只有極微小的改變——譬如地面附近的
自由落體運動 ——重力加速度將幾乎保持不變(參看條目
地心引力 )。而對於一個龐大物體,由於r的變化導致的不同位點所受重力的變化,將會引起巨大而可觀的潮汐力作用。
令m1 為地球質量5.98*102 4 kg,m2 為1kg,R為地球半徑6380000m,代入萬有引力公式,計算出F=9.8N,這說明1kg的物體在地球表面受重力為9.8N。換句話說,等式兩邊同除以m2 ,結果就是重力加速度g。
具有空間廣度的物體:
如果被討論的物體具有空間廣度(遠大於理論上的
質點 ),它們之間的萬有引力可以以物體的各個等效質點所受萬有引力之和來計算。在極限上,當組成質點趨近於“無限小”時,將需要求出兩物體間的力(矢量式見下文)在空間範圍上的積分。
從這裡可以得出:如果物體的質量分布呈現均勻球狀時,其對外界物體施加的萬有引力吸引作用將同所有的質量集中在該物體的
幾何中心 原理時的情況相同。(這不適用於非球狀對稱物體)。
矢量 式:
地球附近空間內的重力示意圖:在此數量級上地球表面的彎曲可被忽略不計,因此力線可以近似地相互平行並且指向地球的中心牛頓萬有引力定律亦可通過矢量方程的形式進行表述而用以計算萬有引力的方向和大小。在下列公式中,以粗體顯示的量代表矢量。
地球的重力示意圖 其中:
F1 2 : 物體1對物體2的引力
G: 萬有引力常量
m1 與m2 : 分別為物體1和物體2的質量
r2 1 = | r2 r1 |: 物體2和物體1之間的距離
r2 1= r1 +r2 物體2和物體1之間的距離
: 物體1到物體2的單位矢量
可以看出
矢量 式方程的形式與之前給出的標量式方程相類似,區別僅在於在矢量式中的F是一個矢量,以及在矢量式方程的右端被乘上了相應的單位向量。而且,我們可以看出:F
1 2 = F
2 1 同樣,重力加速度的矢量式方程與其標量式方程相類似。
重力與引力 1.重力是由於地球的吸引而產生的,但能否說萬有引力就是重力呢?分析這個問題應從地球自轉入手。由於地球自轉,地球上的物體隨之做圓周運動,所受的向心力F1 =mrω2 =mRω2 cosa,F1 是引力F提供的,它是F的一個分力,cosa是引力F與赤道面的夾角的餘弦值,F的另一個分力F2 就是物體所受的重力,即F2 =mg。
由此可見,地球對物體的萬有引力是物體受到重力的原因,但重力不完全等於萬有引力,這是因為物體隨地球自轉,需要有一部分萬有引力來提供向心力。
2.重力與萬有引力間的大小關係
在赤道上滿足mg=F-F向(物體受萬有引力和地面對物體的支持力Fn 的作用,其合力充當向心力,Fn 的大小等於物體的重力的大小)。
在地球兩極處,由於F向=0,即mg=F,在其他位置,mg、F與F向 間符合
平行四邊形定則 。同一物體在赤道處重力最小,並隨緯度的增加而增大。
(2)重力、重力加速度與高度的關係
在距地面高度為h的高處,若不考慮地球自轉的影響時,則mg'=F=GMm/(R+h)2 ;而在地面處mg=GMm/R2 。
距地面高為h處,其重力加速度g'=GM/(R+h)2 ,在地面處g=GM/R2 。
在距地面高度為h的軌道上運行的宇宙飛船中,質量為m的物體的重力即為該處受到的萬有引力,即mg'=GmM/(R+h)2 ,但無法用測力計測出其重力。
勻速圓周運動 一個天體環繞另一個中心天體做
勻速圓周運動 。其向心力由萬有引力提供。即F引=GMm/r
2 ≈mg=ma向,而a向=v
2 /r=ω
2 r=vω=(4π
2 /T
2 )r=4π
2 f
2 r,因此套用萬有引力定律解決天體的有關問題,主要有以下幾個度量關係:F引=GMm/r
2 (r為軌道半徑)=mg=ma向=mv
2 /r=mω
2 r=m(4π
2 /T
2 )r=m4π
2 f
2 r.
重力場:
球狀星團 M13 證明重力場的存在。重力場是用於描述在任意空間內某一點的物體每單位質量所受萬有引力的矢量場。而在實際上等於該點物體所受的重力加速度。
以下是一個普適化的矢量式,可被套用於多於兩個物體的情況(例如在地球與月球之間穿行的火箭)的計算。對於兩個物體的情況(比如說物體1是火箭,物體2是地球)來說,我們可以用 替代並用m替代m1 來將重力場表示為:
因此我們可以得到:
該公式不受產生重力場的物體的限制。重力場的單位為力除以質量的單位;在國際單位制上,被規定為N·kg
ㄢ (牛頓每千克)。
天體力學領域 1.計算天體質量
(1)計算地球質量
若不考慮地球自轉,地面上物體所受重力即地球對它的萬有引力
mg=GmM/R2 由此可得地球質量 M=gR2 /G
(2)計算太陽質量
測量地球繞太陽
公轉周期 ,公轉軌道半徑,將軌道看成圓,勻速圓周運動向心力就是萬有引力
即 GMm/R2 =m(2π/T)2 R 地球質量為m, 太陽質量 M=4π2 R3 /GT2
運用類似方法已知人造衛星質量,衛星繞某天體運動的周期和軌道半徑
可算出天體質量
2.估算天體密度
若設某天體半徑R,衛星繞天體表面運行時,軌道半徑為R,
又測得已知運行周期為T
設衛星質量為m 則 GMm/R2 =m(2π/T)2 R 天體質量M=4π2 R3 /GT2
體積V=4πR3 /3 ρ=M/V=3π/GT2
存在問題 簡介
儘管牛頓對重力的描述對於眾多實踐運用來說十分地精確,但它也具有幾大理論問題且被證明是不完全正確的。
理論問題 沒有任何徵兆表明重力的傳送媒介可以被識別出,牛頓自己也對這種無法說明的
超距作用 感到不滿意(參看後文條目“局限性”)。
牛頓的理論需要定義重力可以瞬時傳播。因此給出了古典自然時空觀的假設,這樣亦能使
約翰內斯·克卜勒 所觀測到的角動量守恆成立。但是,這與愛因斯坦的
狹義相對論 理論有直接的衝突,因為狹義相對論定義了速度的極限——
真空 中的光速——在此速度下信號可以被傳送。
觀測問題 牛頓的理論並不能完全地解釋出
水星 在沿其軌道運動到
近日點 時出現的進動現象。牛頓學說的預言(由其它行星的重力拖曳產生)與實際觀察到的進動相比每世紀會出現43弧秒的誤差。
牛頓的理論預言的重力作用下光線的偏折只有實際觀測結果的一半。
廣義相對論 則與觀察結果更為接近。
所有物體的
重力質量 與
慣性質量 相同的這一觀測現象是牛頓的系統所不能解釋的。廣義相對論則將它作為一個基本條件。參看條目等效原理。
理論局限性 當牛頓非凡的工作使萬有引力定律能夠為數學公式所表示後,他仍然不滿於公式中所隱含的“
超距作用 ”觀點。他從來沒有在他的文字中“賦予產生這種能力的原因”。在其它情況下,他使用運動的現象來解釋物體受到不同力的作用的原因,但是對於重力這種情況,他卻無法用實驗方法來確認運動產生了重力。此外,他甚至還拒絕對這個由地面產生的力的起因提出假設,而這一切都違背了科學證據的原則。
牛頓對重力的發現埋葬了“哲學家至今仍在愚蠢地試圖探索自然”(philosophers have hitherto attempted the search of nature in vain)這句所謂的真理,就同他深信著的“有各種因素”使得“各種迄今未知的原因”是所有“自然現象”的基礎。這些基本的現象至今仍在研究中,而且,雖然存在著許多種的假設,最終答案仍然沒有找出。 雖然
愛因斯坦 的假設的確比牛頓的假設更能精確地解釋確定案例中萬有引力的作用效果,但是他也從來沒有在他的理論中為這種能力賦予一個原因。在愛因斯坦的方程式中,“物質告訴空間怎么扭曲,空間告訴物質怎么移動”(matter tells space how to curve, and space tells matter how to move),但是這個完全異於牛頓世界的新的思想,也不能使愛因斯坦所賦予“產生這種能力的原因”比萬有引力定律使牛頓所賦予的原因更能使空間產生扭曲。牛頓自己說:
我還沒有能力去從現象中發現產生這些重力特性的原因,而且我無法臆測……我所解釋的定律和豐富的
天體 運動的計算已經足夠於說明重力的確存在並能產生效果。一個物體可以不通過任何介質穿過真空間的距離對另一個物體產生作用,在此之上它們的活動和力可以傳送自對方,這對於我來說簡直就是一個天大的謬論。因此,我相信,任何有足夠的哲學思維能力的人都不會沉溺於此。I have not yet been able to discover the cause of these properties of gravity from phenomena and I feign no hypotheses... It is enough that gravity does really exist and acts according to the laws I have explained, and that it abundantly serves to account for all the motions of celestial bodies. That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it.
需注意的是,這裡使用的單詞“原因(cause)”並不是“起因(cause)和影響”或者“被告導致(cause)受害者死亡”中所表示的意義。何況,當牛頓使用單詞“原因(cause)”時,他(明顯地)意指為一種“解釋”。或者說,像“牛頓學說的重力是行星運動的原因”這個短語的意思就是牛頓學說的重力解釋了行星的運動。
演化過程 過往理論 亞里士多德 引力理論 亞里士多德認為,物體的運動速度和其所受外界的合力是成正比(或者是該物體所受的自己本身的引力),並且和物體運動介質的粘度成反比。
尼古拉·特斯拉 (Nikola Tesla)宣布但是從未發表的引力動力學理論;部分原因是因為理論的細節(如果有的話)並沒有透露,並沒有得到物理學家們的重視。
感應引力(Induced Gravity),由
安德烈·薩哈羅夫 (Andrei Sakharov)提出,認為廣義相對論可能起源於量子場論。
雷薩吉萬有引力理論(Le Sage's Theory of Gravitation)(也叫做雷薩吉引力理論 ),由喬治-路易斯·雷薩吉(Georges-Louis Le Sage)提出,以一種充滿整個宇宙輕的氣體的流動來解釋這種現象。
萬有引力理論(Nordström's Theory of Gravitation),
廣義相對論 的早期競爭者。
懷特黑德 萬有引力理論,(Whitehead's Theory of Gravitation)廣義相對論的另一個早期競爭者。
牛頓的萬有引力定律 存在於任何兩個物體之間的由質量引起的相互吸引力,力的作用線約在兩物體質心的連線上,其大小與兩物體的質量成正比,與兩物體的距離平方成反比。萬有引力定律是牛頓追索地面上的物體受重力作用的原因而發現的,1687年正式發表。以
m 1 、
m 2 表示兩物體的質量,
r 表示兩者之間的距離,則相互吸引的力
F 為:
,式中
G 稱為萬有引力常數。這就是萬有引力定律的數學表達式。嚴格地說,上式是對兩質點而言的。因為“兩個物體之間的距離”一語指的是兩個質點的距離。如果一個是質點,另一個是有限體,則可把有限體分割成許多質點,並求出它們引力的矢量和,就能得到整個有限體對質點的作用力。牛頓曾證明:一個密度是到球心距離
r 的函式的球體對球外一質點的引力同整個球體質量集中在球心的情況無異。牛頓用萬有引力定律證明了克卜勒定律、月球繞地球的運動、潮汐的成因和地球兩極較扁等自然現象。牛頓的萬有引力定律是天體力學的基礎。人造衛星、月球和行星探測器的軌道,都是以這個定律為基礎來計算的。萬有引力存在的實驗證明和引力常數
G 的測定是卡文迪什於1798年作出的。目前引力常數的公認值是G=6.6732×10
- 1 1 m
2 /kg·s
2 。
廣義相對論 1859年,法國天文學家勒威耶發現水星近日點進動速率的數值與用萬有引力定律算得的數值有每百年38″(美國天文學家S.紐康的測定值為43″)的偏離。1915年,愛因斯坦創立廣義相對論,終於說明了這個問題,並預言光線在引力場中的偏折和光譜的紅移。天文學家還曾預言黑洞的存在,使廣義相對論進入了與宇宙演化有關的新境界。愛因斯坦以加速坐標系和引力場的等效性否定了慣性坐標系在宇宙空間的存在,又用引力場改變了空間特性。他認為物體在引力場的運動是沿四維彎曲的黎曼空間的短程線。但是在弱引力場的情況(例如太陽系)下,對許多力學問題,用牛頓萬有引力定律比用愛因斯坦的廣義相對論計算要簡單得多,而且兩者相差極微。對簡單的二體問題,由於“同時”概念混雜,難以用廣義相對論進行數學處理。
在粒子相互作用的微觀世界裡,萬有引力是最弱的—種,萬有引力與電磁力、核力的統一問題有待於科學家們的進一步努力。
參考文獻 1、詞條作者:汪家訸.《中國大百科全書》74卷(第一版)力學 詞條:萬有引力:中國大百科全書出版社,1987 :490頁.

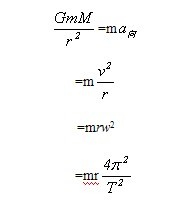


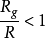


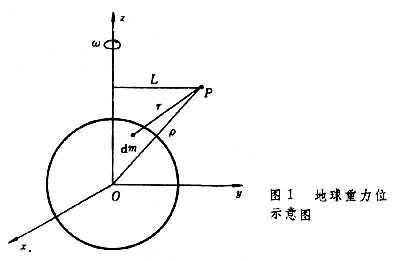 地球的重力示意圖
地球的重力示意圖