基本介紹
- 中文名:牛頓位勢
- 外文名:Newton potential
- 屬性:一般位勢的經典模型之一
- 所屬學科:數學(位勢論)
- 相關概念:位勢,牛頓核等
基本介紹












廣義函式的牛頓位勢









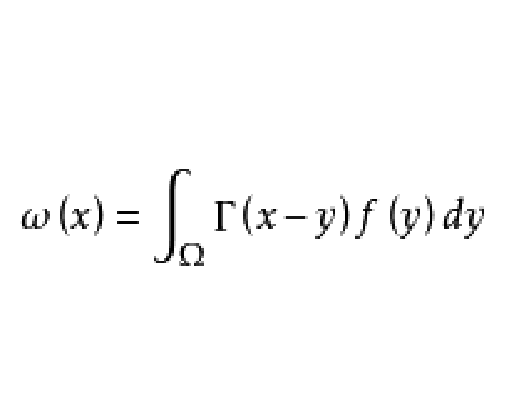





















牛頓位勢(Newton potential)是一般位勢的經典模型之一。在Rn(n≥3)中,2核K=|x-y|2-n稱為牛頓核,相應的位勢稱為牛頓位勢。當n=3時,據牛頓萬有引力公式...
一般位勢是經典位勢的一種直接推廣形式,常為一個二元數值函式(核)關於某個測度的積分。...
所謂經典位勢論,是指研究經典位勢及其關聯的調和函式、上(下)調和函式等的性質及其套用的理論,也稱為關於拉普拉斯方程的位勢論。...
平衡原理(equilibrium principle)是靜電學中平衡問題的數學描述。在經典位勢論中,平衡問題(即對經典位勢如何確定上述的測度μ)與掃除問題、狄利克雷問題被列為位勢...
迭核(iterated kernel)是由已知核經過逐次積分而得到的各種核。核是位勢論的基本概念。在位勢論中,所謂核,常指一般位勢的核。這時若K(x,y)≥0恆成立,則稱...
微積分的創立,本來就有物理方面的源泉,所以分析學與物理的緊密聯繫從牛頓時代就開始了。以後在不同時代建立的一些分析學科(如變分法、位勢論等)發展了這種關係。...
位勢論起源於物理學的萬有引力學說和靜電學,遠在1733年,拉格朗日(Lagrange,J.-L.)就注意到引力場是一個函式(稱為牛頓位勢)的梯度。在三維歐氏空間,一個單位...
就注意到引力場是一個函式(稱為牛頓位勢)的梯度。1925年,里斯(Riesz,F.)引進了上(下)調和函式的概念,為位勢論研究提供了新的方法;里斯分解定理建立了上調和...
V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:7次歷史版本 最近更新: 創建者:牛頓位勢猜你關注新手上路 成長任務 編輯入門 編輯規則 百科術語 我有疑問 我要...
第11章 高維布朗運動與牛頓位勢/2 11.1 勢論大意/3 11.2 布朗運動略述/7 11.3 首中時與首中點/14 11.4 調和函式/21 11.5 Dirichlet問題/26...
V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次歷史版本 最近更新: 創建者:牛頓位勢猜你喜歡新手上路 成長任務 編輯入門 編輯規則 百科術語...
圖集 3G服務:創建殺手級套用圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:3次歷史版本 最近更新: 創建者:牛頓位勢猜你喜歡...
19、 論文《一類帶有非牛頓位勢的可壓縮Navier-Stokes方程整體強解的存在性》,發表在數學年刊,A輯,2011第4期;20、 論文《Global existence of strong solutions ...
