無窮質點馬爾可夫過程(Markov processes withinfinite particles)一類重要的馬爾可夫過程.如果其狀態空間X為卿‘上的拉東(Radon)計數測度空間(即在緊集上質點數目有窮),則該馬爾可夫過程稱為無窮質點馬爾可夫過程。
基本介紹
- 中文名:無窮質點馬爾可夫過程
- 外文名:Markov processes withinfinite particles
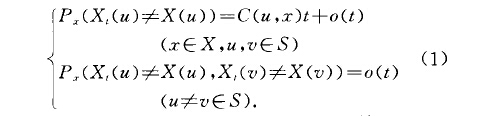
無窮質點馬爾可夫過程(Markov processes withinfinite particles)一類重要的馬爾可夫過程.如果其狀態空間X為卿‘上的拉東(Radon)計數測度空間(即在緊集上質點數目有窮),則該馬爾可夫過程稱為無窮質點馬爾可夫過程。
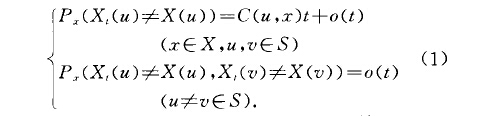
無窮質點馬爾可夫過程(Markov processes withinfinite particles)一類重要的馬爾可夫過程.如果其狀態空間X為卿‘上的拉東(Radon)計數測度空間(即在緊集上質點數目有窮),則該馬爾可...
無窮質點馬爾可夫過程雖然是由平衡統計物理引起的,但近年來不斷提出了新的模型。這些模型涉及非平衡統計物理、化學、生物、醫學以及社會科學。它的研究已進入非平衡系統的範圍,遍歷性理論是它的主要研究方向。這是機率論中一個值得注意的...
《隨機環境中的無窮質點系統》是陳大岳為項目負責人,北京大學為依託單位的青年科學基金項目。項目摘要 過去三年的研究工作主要是有關無窮粒子系統的問題,也研究一般離散狀態空間的馬爾可夫過程。針對隨機伊辛模型中的問題,推廣了Freidlin-...
主要內容有:多指標隨機過程、無窮質點與馬爾可夫過程、機率與位勢及各種特殊過程的專題討論等。中國學者在平穩過程、馬爾科夫過程、鞅論、極限定理、隨機微分方程等方面做出了較好的工作。數學上的隨機過程是由實際隨機過程概念引起的一種...
無窮質點馬爾可夫過程(Markov processes withinfinite particles)一類重要的馬爾可夫過程.如果其狀態空間X為卿‘上的拉東(Radon)計數測度空間(即在緊集上質點數目有窮),則該馬爾可夫過程稱為無窮質點馬爾可夫過程。無窮質點馬爾可夫過程源於統計...
與人合作建立了非平衡統計物理的一般機率模型,開展隨機場與無窮質點馬爾可夫過程的研究。“無窮質點馬爾可夫過程與Q過程”1985年獲國家教委科技進步獎二等獎。嚴士健是一位在代數、數論和機率論等領域的科學研究及教學中做出重要貢獻的數學家...
