滲流方程(filtration equation)是指一個描述流體在多孔介質中運動的方程。
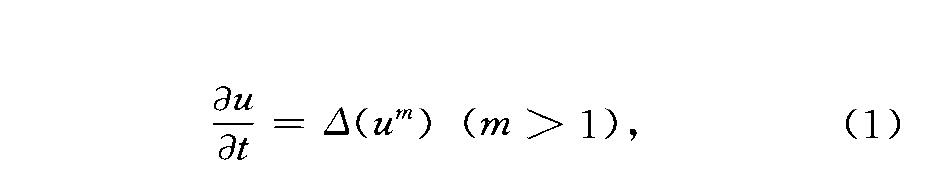
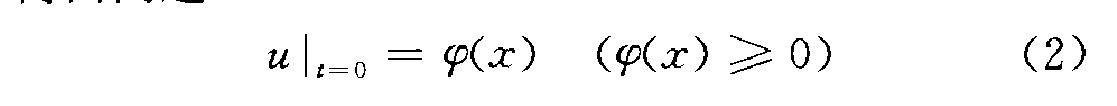
滲流方程(filtration equation)是指一個描述流體在多孔介質中運動的方程。
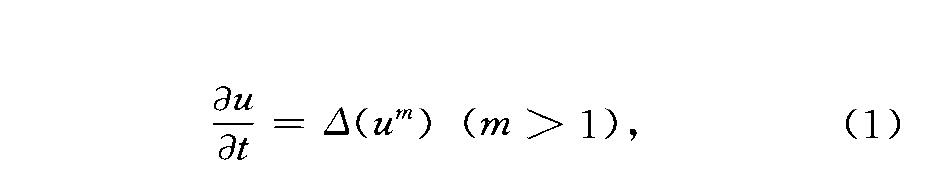
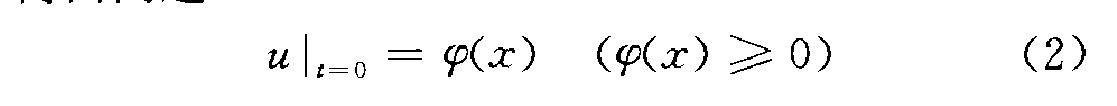
滲流方程(filtration equation)是指一個描述流體在多孔介質中運動的方程。... 滲流方程(filtration equation)是指一個描述流體在多孔介質中運動的方程。
這種簡單條件下的滲流問題的數學模型是拉普拉斯方程,傅立葉熱傳導方程和二階非線性拋物型方程。這個階段的研究方法主要是數學物理方法和比較簡單的模擬方法。現代滲流...
Kozeny-Carman方程是一種表示岩石滲透率與孔隙度和岩石比面之間關係的公式。... kozeny-carman(KC)方程是多孔介質滲流領域最著名的半經驗公式,長期以來,KC方程及其...
土中滲流是指水或其他流體在土體孔隙中的流動。土中滲流性質決定於土的顆粒組成和流體的性質。由於土體孔隙的大小、形狀及其分布異常複雜,很難像地表水流動那樣尋求...
液體滲流是承壓條件下均質液體在多孔介質中的流動。... 定常滲流的數學模型是拉普拉斯方程,弱彈性液體不定常滲流的數學模型是傅立葉熱傳導方程。 早期的石油和地下...
包括滲透性、滲流理論、滲流應力狀態和滲流控制等。對大多數岩石假定岩石中的水流為層流,流速與水力梯度呈線性關係,遵循達西定律。岩石滲透性用滲透係數表示,該係數...
氣體滲流是指氣體在多孔介質中的流動。氣體流動的特殊性主要表現在氣體壓縮性的影響、非達西流動(見達西滲流定律)和非等溫流動的影響以及滑脫效應等。...
《地下水滲流力學》是2013年水利水電出版社出版的圖書,作者是王俊傑。... 全書共10章,內容包括:水力學基礎、地下水滲流力學基礎、地下水滲流微分方程、河渠地下水...
如相對論流體力學,多孔介質流體力學(即滲流力學)、稀薄氣體動力學、非平衡系統流體力學、多相流體力學、非牛頓流體力學、電流體動力學、磁流體力學、物理-化學流體...
《地下水運動方程》是2011年地質出版社出版的圖書,作者是王旭升,萬力。... 共7章,內容包括經典地下水動力學和滲流力學的基本方程、偏微分方程定解問題的構成等 [...
不溶混的兩種液體在多孔介質中的驅替式流動。它是滲流力學研究的基本流動之一,是天然水驅開發油田和人工注水開發油田中常見的流動。...
1960年蘇聯巴倫布拉特和熱爾托夫針對上述雙重介質的特點,建立了在這種介質中弱壓縮液體不定常滲流的數學模型(二元線性拋物型偏微分方程組)。經過各國學者近二十年的...
kozeny-carman(KC)方程是多孔介質滲流領域最著名的半經驗公式,長期以來,KC方程及其推廣形式被廣泛用於估算多孔介質的滲透率。KC方程不僅在地下滲流、油氣田開採、化學...
混氣液體滲流是指液體與氣體(氣泡)摻混在一起的流體通過多孔介質的流動。... 根據各相流體滲流的運動方程(達西滲流定律)和連續性方程,可得到混氣液體滲流的非...
程林松編著的《滲流力學》從滲流基本規律及滲流數學模型入手,系統介紹了單相不可壓縮流體的穩定滲流規律,水壓驅動方式下多井工作時的干擾理論,油水和油氣兩相滲流理論...
《高等滲流力學 (第2版)》是2010年出版的圖書,作者是孔祥言。... 6 氣體滲流理論6.1 天然氣的物理特性6.2 氣體滲流方程6.3 氣體穩態滲流6.4 鉛直氣井非穩態...
水壩滲流問題(filtration problem in dam)亦 稱浸潤面問題一個經典的工程力學問題.考慮一個 分離兩個水庫的土壩.設壩體無限延伸,具有可滲透 側壁和不可滲透底部....
《劉慈群滲流力學論文集》是2010-11-01石油工業出版社出版的圖書,作者是劉慈群... 16 三重介質彈性滲流方程組的精確解17 雙重介質非線性滲流18 雙重介質中彈性...
根據質量守恆原則,可求得以θ和h為變數的兩個一維垂向滲流微分方程:式中 為非飽水土的擴散度; 為非飽水土的容水度;t為時間變數。
《低滲透多孔介質滲流的動邊界理論》是2018年科學出版社出版的圖書,作者是劉文超。... 連續性方程中非線性項對動邊界模型計算結果的影響,並將低滲透多孔介質滲流動...
《滲流力學基礎實驗指導書》是2018年中國地質大學出版社出版的圖書,作者是潘琳。... 《滲流力學基礎實驗指導書》是2018年中國地質大學出版社出版的圖書,作者是潘琳。
在實際工程中一維固結問題非常少見,大多是二維固結或三維固結情況,二維固結和三維固結常稱為多維固結。在多維固結問題中,水的滲流和土體的變形都是多維的。為了求解...
達西定律(Darcy's law)描述飽和土中水的滲流速度與水力坡降之間的線性關係的規律,又稱線性滲流定律。1856年由法國工程師H.P.G.達西通過實驗總結得到。1852-1855...
比奧固結理論建立方程所依據的假定比較 相同點:假設骨架線性彈性,變形微小,滲流符合達西定律等。不同點:太沙基認為在固結過程中法向總應力和H不隨時間而變,而...
將描述地下滲流的水相方程及氣相方程和由滲流作用引起的岩(土)體的變形方程耦合起來,引入飽和度和相對滲透率的概念,採用全隱式聯立求解方法,實現了解的無條件穩定...
