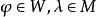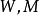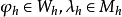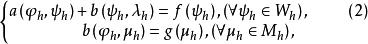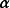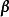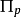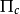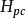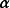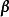混合有限元法

混合有限元法(mixed finite element method) 結構分析中同時取節點位移向量和節點內力向量作為獨立場變數的一種有限元法。此法通過節點位移向量和內力向量表示單元內部的位移場和應力場，再套用廣義變分原理就可得到混合模型(即位移模型與應力模型的混合，或協調模型與平衡模型的混合)。混合有限元法的優點是選用插值函式比較簡單，缺點是最後得出的聯立方程組的係數矩陣不是正定的，從而在一定程度上限制了該法的廣泛套用。

基本介紹

• 中文名：混合有限元法
• 外文名：mixed finite element method
• 所屬學科：數學、物理
• 原理：混合變分原理
• 相關概念：雙線性泛函、希爾伯特空間等

方法介紹

混合有限元法(mixed finite element method)是一種有限元法，是基於混合變分原理的有限元方法。混合有限元法的特點是同時選擇兩個基本未知函式，即位移函式和力函式。套用混合能量原理推導出混合有限元法基本方程。

在混合變分原理中，未知函式除函式值本身外還有函式的導數，於是，混合有限元方法不僅要計算函式本身的近似值，同時也計算導數的近似值，因此適於需要計算函式本身及導數的科學與工程計算問題，高階方程可由降階以後再化為混合變分問題求解，故該方法適於高階方程求解，考慮混合變分問題：

求 ，使

其中W，M是兩個希爾伯特空間， 是定義在W×W上的連續雙線性泛函，且是強制的， 是定義在W×M上的連續雙線性泛函， (W的對偶空間)， (M的對偶空間)，設 分別為 的某一有限元子空間，則下述離散問題稱為(1)的混合有限元逼近：

求 ，使

若雙線性泛函 是連續且強制的；雙線性泛函 是連續的，且

其中β是正的常數，則問題(2)存在惟一解(φ_h，λ_h)，且

條件(3)稱為LBB條件，它取自拉德仁斯卡婭(Лaдыжкенская，О.А.)(1949)，巴布希卡 及布雷齊(Brezzi，F.)(1974)姓名的第一個字母。

混合分區變分原理

混合模型或雜交模型只是在單元水平上採用混合法，而混合分區變分原理則是在結構整體水平上採用混合法。混合分區變分原理在理論上解決了兩類不同區域(余能區、勢能區)和兩類不同單元(應力元、位移元)並存及其耦合和收斂問題，在實際套用上(如求解含有應力集中的問題)是非常成功的。成功的原因是巧妙地把應力元與位移元、奇異元與常規元、解析解與數值解相結合，使每一種方法在各自的分區範圍內發揮其長處，從而獲得整體上的最佳效果。

混合分區變分原理構成了混合有限元法的基礎，其特點是將彈性體劃分為勢能區單元和余能區單元的混合分區體系，以勢能區的節點位移和余能區的應力參數作為基本未知量，套用混合分區變分原理導出分區混合有限元法的基本方程，並用於求解上述混合型基本變數。

套用混合分區變分原理：

=駐值 (4)

式中 是勢能區的位移參數， 是余能區的應力參數， 是勢能區的總勢能， 是余能區的總余能， 是余能區和勢能區交界面的附加能量。

由駐值條件

導出混合有限元法的基本方程，解出位移參數 和應力參數 。