基本介紹
- 中文名:海廷代數
- 分類:格理論、代數邏輯
- 領域:數理科學
形式定義


等價定義





性質















例子


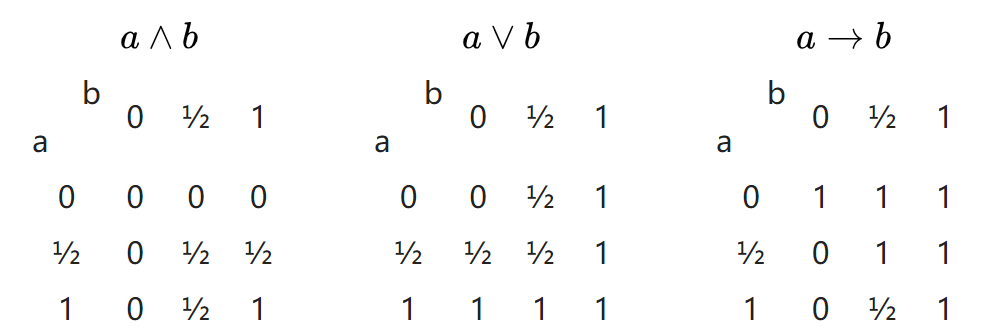

































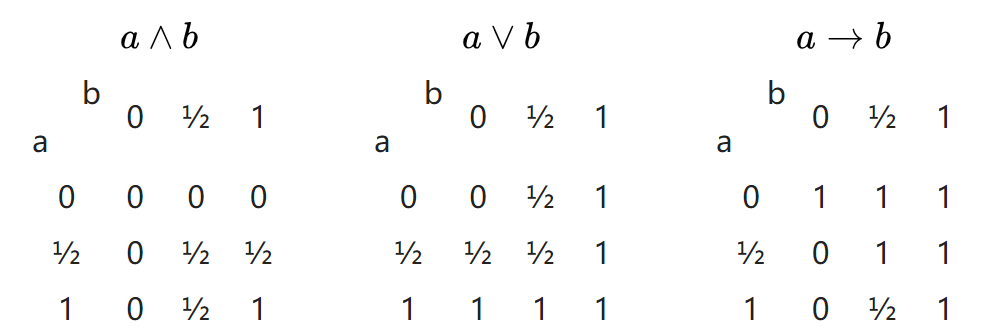








在數學裡,海廷代數是一特殊的偏序集,經由廣義化布爾代數而成,得名於阿蘭德·海廷。海廷代數是作為直覺主義邏輯的模型而產生的,是一種排中律不總是成立的邏輯。完全海廷代數是無點拓撲學的核心。形式定義海廷代數H為一有界格,滿足如...
P是海廷代數,就是說運算 (x - )有一個右伴隨(也叫做(單調)伽羅瓦連線的下伴隨),對於每個P的元素x。對於所有P的元素x和所有P的子集S,下列無限分配律成立:P是分配格,就是說對於所有P中的x,y和z,有著 並且P是交連續...
因為兩個定義是等價的,格論可以從序理論和泛代數兩個角度來理解。具體格的例子有海廷代數和布爾代數。格 格是一種特殊的偏序集,對其中任意兩個元素都可取最小上界( )和最大下界( )。格中的運算律 設L是格,a,b,c L,則...
內部代數 在抽象代數中,內部代數是採用了集合的拓撲內部概念的特定類型的代數結構。內部代數之對於拓撲和模態邏輯S4如同布爾代數之對於集合論和普通命題邏輯。內部代數形成了模態代數的一個簇。參見 內部代數 海廷代數 ...
在代數上說,集合{真, 假}形成了簡單的布爾代數。可以把其他布爾代數用作多值邏輯中的真值集合,但直覺主義邏輯把布爾代數推廣為海廷代數。在topos理論中,topos的主客對象分類器接管了真值集合的位置。布爾值函式 布爾值函式是 類型的...
格也可以特徵化為滿足特定公理恆等式的代數結構。因為兩個定義是等價的,格理論從序理論和泛代數二者提取內容。半格包括了格,依次包括海廷代數和布爾代數。這些"格樣式"的結構都允許序理論和抽象代數的描述。參見 域理論 偏序關係 全序...
研究了代數系統的理論結構表示,這種系統滿足海廷公理。在可結合代數方面,他提出了著名的伯克霍夫一維特(E.Witt)關於李代數的可表示性定理。他還研究了一般拓撲學中的穆爾-史密斯收斂性。其主要著作有《格論》(1940)、《近世代數概論...
半格包括了格,依次包括海廷代數和布爾代數。這些"格樣式"的結構都允許序理論和抽象代數的描述。拓撲學 在數學裡,拓撲學(英語:topology),或意譯為位相幾何學,是一門研究拓撲空間的學科,主要研究空間內,在連續變化(如拉伸或彎曲...
半格包括了格,依次包括海廷代數和布爾代數。這些"格樣式"的結構都允許序理論和抽象代數的描述。考慮任意一個偏序集合(L,≤),如果對集合L中的任意元素a,b,使得a,b在L中存在一個最大下界,和最小上界,則(L,≤)是一個格。這...
