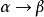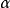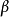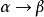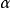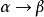基本介紹
- 中文名:柯里-霍華德同構
- 外文名:Curry-Howard Isomorphism
- 學科:計算機計算理論
- 意義:揭示電腦程式和數學證明聯繫
- 別名:公式為類型對應或命題為類型對應
- 發現者:哈斯凱爾·加里
簡介,對應的起源、範圍和結論,程式語言與證明,類型,相繼式演算,
簡介
Curry-Howard 同構顯示了推理系統和程式語言之間的相似性,類型即命題,程式即證明。或表示了電腦程式與數理邏輯之間的直接聯繫(邏輯上的等價關係),即我們可以利用數理邏輯中的某些東西來去表示程式中的特定邏輯。
在此框架下:程式語言的語言構造同構為推理系統的推理規則、程式的類型同構為邏輯命題、閉合程式(不依賴環境的程式)可以同構為一條定理的證明過程,其類型就是一條定理以及邏輯上下文同構為自由變數類型指派。例如Lambda 演算同構為 Gentzen 的自然演繹:
- 函式調用就是蘊含消除
- 函式抽象就是蘊含介入
- 參數多態就是全稱量化
- 模板類型就是謂詞
- 結構類型就是合取
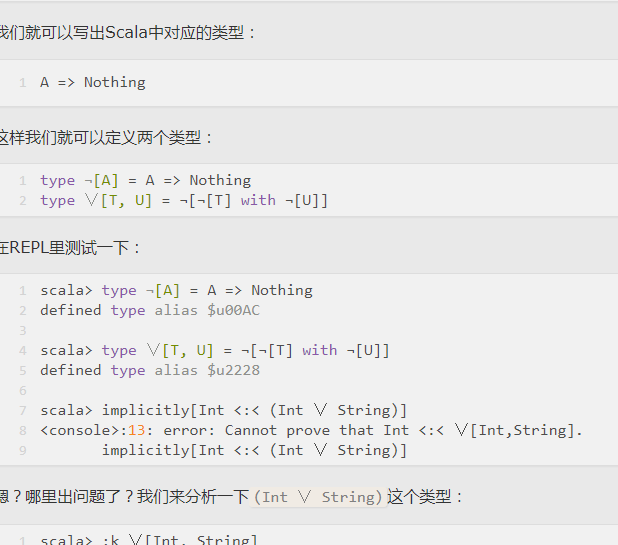
- 聯合類型就是析取
- 收參數但不返回就是否定
- 高洋上的 call/cc 就是雙重否定消除
對應的起源、範圍和結論
對應可以在兩個層面上看到,首先是類比層次,它聲稱對一個函式計算出的值的類型的斷言可類比於一個邏輯定理,計算這個值的程式可類比於這個定理的證明。在理論計算機科學中,這是連線λ演算和類型論的毗鄰領域的一個重要的底層原理。它被經常以下列形式陳述為“證明是程式”。一個可選擇的形式化為“命題為類型”。其次,更加正式的,它指定了在兩個數學領域之間的同構,就是以一種特定方式形式化的自然演繹和簡單類型λ演算之間是雙射,首先是證明和項,其次是證明歸約步驟和beta歸約。
有多種方式考慮柯里-霍華德對應。在一個方向上,它工作於“把證明編譯為程式”級別上。這裡的“證明”最初被限定為在構造性邏輯中—典型的是直覺邏輯系統中的證明。而“程式”是在常規的函式式編程的意義上的;從語法的觀點上看,這種程式是用某種λ演算表達的。所以柯里-霍華德同構的具體實現是詳細研究如何把來自直覺邏輯的證明寫成λ項。(這是霍華德的貢獻;柯里貢獻了組合子,它是相對於是高級語言的λ演算是能寫所有東西的機器語言)。最近,同樣處理經典邏輯的柯里-霍華德對應的擴展可被公式化了,通過對經典有效規則比如雙重否定除去和皮爾士定律關聯上明確的用續體比如call/cc處理的一類項。
還有一個相反的方向,對一個程式的正確性關聯上“證明提取”的可能性。這在非常豐富的類型論環境中是可行的。實際上理論家對推進非常豐富類型的函式式程式語言的開發的動機,已經部分地混合了希望帶給柯里-霍華德對應更加顯著的地位的因素。
程式語言與證明
程式語言
程式語言是用來定義計算機指令執行流程的形式化語言。每種程式語言都包含一整套辭彙和語法規範。這些規範通常包括數據類型和數據結構、指令類型和指令控制、調用機制和庫函式以及不成文的規定(如遞進書寫、變數命名等)。每一種程式設計語言可以被看作是一套包含語法、辭彙和含義的正式規範。這些規範通常包括:數據和數據結構、指令及流程控制、引用機制和重用以及設計哲學。語法是說明程式語言中,哪些符號或文字的組合方式是正確的,語義則是對於編程的解釋。
數學證明
數學上的證明包括兩個不同的概念。首先是非形式化的證明:一種以自然語言寫成的嚴密論證,用來說服聽眾或讀者去接受某個定理或論斷的真確性。由於這種證明使用了自然語言,因此對於非形式化證明在嚴謹性上的標準,將取決於聽眾或讀者對課題的理解程度。非形式化證明在大多數的套用場合中出現,例如科普講座、口頭辯論、初等教育或高等教育的某些部分。有時候非形式化的證明被稱作“正式的”,但這只是強調其中論證的嚴謹性。而當邏輯學家使用“正式證明”一詞時,指的是另一種完全不同的證明——形式化證明。
在數理邏輯中,形式化證明並不是以自然語言書寫,而是以形式化的語言書寫:這種語言包含了由一個給定的字母表中的字元所構成的字元串。而證明則是一種由該些字元串組成的有限長度的序列。這種定義使得人們可以談論嚴格意義上的“證明”,而不涉及任何邏輯上的模糊之處。研究證明的形式化和公理化的理論稱為證明論。儘管理論上來說,每個非形式化的證明都可以轉化為形式化證明,但實際中很少會這樣做。對形式化證明的研究主要套用在探討關於可證明性的一般性質,或說明某些命題的不可證明性等等。
類型
依據 演算,我們將使用
演算,我們將使用 來指示帶有形式參數x和函式體
來指示帶有形式參數x和函式體 的函式。在套用於參數比如
的函式。在套用於參數比如 的時候,這個函式生成E,並帶有x的所有自由出現都被替換為
的時候,這個函式生成E,並帶有x的所有自由出現都被替換為 。有效的
。有效的 演算表達式有如下形式之一:
演算表達式有如下形式之一:






1、 (這裡的
(這裡的 是個變數)
是個變數)


2、
 (這裡的是
(這裡的是 個變數,而E是個演算表達式)
個變數,而E是個演算表達式)



3、(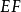 )(這裡的
)(這裡的 和F是
和F是 演算表達式)
演算表達式)
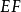


通常我們將縮寫(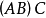 )為(
)為( ),縮寫
),縮寫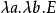 為
為 。一個表達式被稱為是“閉合的”,如果它不包含自由變數。
。一個表達式被稱為是“閉合的”,如果它不包含自由變數。
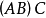

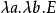

類型確定規則
類型可以依賴於類型變數,它被指示為小寫的希臘字母 ,
,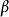 等等。在我們概念中類型變數是被隱含的全稱量化的,就是說,如果一個值有包括類型變數的一個類型,則它必須由這個類型變數的所有可能實例組成。我們可以定義任意表達式的類型為如下:
等等。在我們概念中類型變數是被隱含的全稱量化的,就是說,如果一個值有包括類型變數的一個類型,則它必須由這個類型變數的所有可能實例組成。我們可以定義任意表達式的類型為如下:

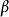
1、一個變數比如 可以有任意類型。
可以有任意類型。

2、如果變數有類型 ,而表達式
,而表達式 有類型
有類型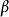 ,則
,則 有指示為的類型;就是說,它是取類型
有指示為的類型;就是說,它是取類型 的值,並映射到類型
的值,並映射到類型 的值。
的值。


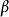



3、在表達式( )中,如果F有類型
)中,如果F有類型 ,則E必須有類型
,則E必須有類型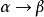 (就是說它必須是期望類型的參數的函式)並且這個表達式有類型
(就是說它必須是期望類型的參數的函式)並且這個表達式有類型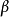 。
。


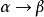
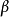
例如,考慮函式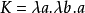 。假定
。假定 有類型
有類型 而b有類型
而b有類型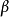 。則
。則
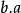 有類型
有類型 ,而
,而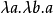 有類型
有類型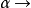 (
(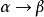 )。我們接受→是右結合的約定,所以這個類型也可以寫為
)。我們接受→是右結合的約定,所以這個類型也可以寫為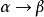
 。這意味著K函式接受類型α的參數並返回一個函式,它接受類型β的參數並返回類型
。這意味著K函式接受類型α的參數並返回一個函式,它接受類型β的參數並返回類型 的值。
的值。
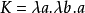


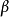

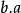

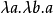
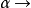
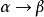
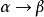


類型居留問題
很明顯 -表達式可以有非常複雜的類型。你可能要問是否有帶有給定類型的
-表達式可以有非常複雜的類型。你可能要問是否有帶有給定類型的 -表達式。找到帶有特定類型的
-表達式。找到帶有特定類型的 -表達式的問題叫做類型居留問題。
-表達式的問題叫做類型居留問題。



答案是非常引人注目的:有帶有特定類型的閉合 -表達式,若且唯若這個類型對應於一個邏輯定理,在這裡的→符號再次解釋為意味著邏輯蘊涵的時候。
-表達式,若且唯若這個類型對應於一個邏輯定理,在這裡的→符號再次解釋為意味著邏輯蘊涵的時候。

例如,考慮恆等函式
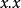 ,它接受類型ξ的參數並返回類型ξ的結果,所以有類型
,它接受類型ξ的參數並返回類型ξ的結果,所以有類型 。
。 當然是邏輯定理:給定一個公式
當然是邏輯定理:給定一個公式 ,你可以結論出
,你可以結論出 。
。

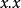




K函式的類型 也是一個定理。如果已知
也是一個定理。如果已知 為真,則你可以結論出如果
為真,則你可以結論出如果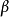 為真就能推出
為真就能推出 。這有時也叫做重複規則。B的類型是 (
。這有時也叫做重複規則。B的類型是 (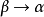 )→(
)→( )
) 。你可類似的把它解釋為邏輯重言式;如果已知(
。你可類似的把它解釋為邏輯重言式;如果已知(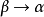 )為真,則如果已知(
)為真,則如果已知( )為真,你就能推出
)為真,你就能推出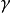 蘊涵
蘊涵 。
。


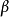

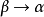


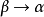

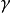

相繼式演算
在證明論和數理邏輯中,相繼式演算(又譯矢列演算、矢列式演算)是眾所周知的一階邏輯(和作為它的特殊情況的命題邏輯)的演繹系統。這個系統也叫做 系統,用以區別於後來建立的有時也叫做相繼式演算的類似風格的各種其他系統。另一個給這種系統的術語是Gentzen系統。相繼式演算
系統,用以區別於後來建立的有時也叫做相繼式演算的類似風格的各種其他系統。另一個給這種系統的術語是Gentzen系統。相繼式演算 由Gerhard Gentzen介入為研究自然演繹的工具。它已經變成構造邏輯推導的非常有用的演算。它的名字得來自德語的Logischer Kalkül,意思是"邏輯演算"。相繼式演算是關於這個主題的很多研究所選擇的方法。
由Gerhard Gentzen介入為研究自然演繹的工具。它已經變成構造邏輯推導的非常有用的演算。它的名字得來自德語的Logischer Kalkül,意思是"邏輯演算"。相繼式演算是關於這個主題的很多研究所選擇的方法。


證明邏輯定理的更加直覺的方式是根岑的相繼式演算。相繼式演算以同希爾伯特式證明對應於組合子表達式一樣的方式對應於λ-表達式程式。直覺邏輯的蘊涵片段的相繼式演算規則是:



Γ表示上下文,它是假設的集合。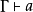 指示假定上下文Γ我們可以證明
指示假定上下文Γ我們可以證明 。邏輯定理完全由其證明不需要假設的那些公式t組成的;就是說,t是一個定理,若且唯若我們可以證明
。邏輯定理完全由其證明不需要假設的那些公式t組成的;就是說,t是一個定理,若且唯若我們可以證明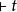 。
。
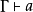

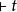
在相繼式演算中的證明是樹,它的根是我們要證明的定理,而它的葉子是公理模式實例;每個內部節點必須標記為要么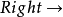 要么
要么 ,並且必須包含依據指定規則從子節點推出的一個公式。
,並且必須包含依據指定規則從子節點推出的一個公式。
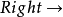

相繼式演算證明緊密的對應於λ-演算表達式。斷言 可以被解釋為意味著,給定帶有在Γ中列出類型的值,我們可以製造帶有類型
可以被解釋為意味著,給定帶有在Γ中列出類型的值,我們可以製造帶有類型 的一個值。公理對應於帶有新的無約束的類型的新變數介入。
的一個值。公理對應於帶有新的無約束的類型的新變數介入。 規則對應於函式抽象:
規則對應於函式抽象: