在簡單類型lambda演算中，類型居留問題是如下問題: 給定一個類型τ，是否存在一個λ-項 M 使得對於某個類型環境γ有Γ M：τ? 如果回答是肯定的，則 M 被稱為τ的居所。
因為在簡單類型的 lambda 演算中類型對應於極小蘊涵邏輯(參見Curry-Howard同構)，一個類型有一個居所，若且唯若它是極小蘊涵邏輯的重言式。
基本介紹
- 中文名：類型居留問題
- 外文名：Type inhabitation
簡介,簡單類型λ演算,柯里-霍華德同構,對應的起源、範圍和結論,
簡介
在簡單類型lambda演算中，類型居留問題是如下問題: 給定一個類型τ，是否存在一個λ-項 M 使得對於某個類型環境γ有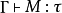
? 如果回答是肯定的，則 M 被稱為τ的居所。
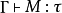
因為在簡單類型的 lambda 演算中類型對應於極小蘊涵邏輯(參見Curry-Howard同構)，一個類型有一個居所，若且唯若它是極小蘊涵邏輯的重言式。
Richard Statman證明了類型居留問題是PSPACE-完全性的。
簡單類型λ演算
簡單類型 lambda 演算(
)是連線詞只有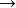
(函式類型)的有類型 lambda 演算。這使它成為規範的、在很多方面是最簡單的有類型 lambda 演算的例子。
簡單類型也被用來稱呼對簡單類型 lambda 演算的擴展比如積、陪積或自然數(系統 T)甚至完全的遞歸(如PCF)。相反的，介入了多態類型(如系統F)或依賴類型(如邏輯框架)的系統不被當作是簡單類型。簡單類型 lambda 演算最初由阿隆佐·邱奇在 1940 年介入來嘗試避免無類型 lambda 演算的悖論性使用。
柯里-霍華德同構
柯里-霍華德對應是在電腦程式和數學證明之間的緊密聯繫；這種對應也叫做柯里-霍華德同構、公式為類型對應或命題為類型對應。這是對形式邏輯系統和公式計算（computational calculus）之間符號的相似性的推廣。它被認為是由美國數學家哈斯凱爾·加里和邏輯學家William Alvin Howard獨立發現的。
對應的起源、範圍和結論
對應可以在兩個層面上看到，首先是類比層次，它聲稱對一個函式計算出的值的類型的斷言可類比於一個邏輯定理，計算這個值的程式可類比於這個定理的證明。在理論計算機科學中，這是連線λ演算和類型論的毗鄰領域的一個重要的底層原理。它被經常以下列形式陳述為“證明是程式”。一個可選擇的形式化為“命題為類型”。其次，更加正式的，它指定了在兩個數學領域之間的同構，就是以一種特定方式形式化的自然演繹和簡單類型λ演算之間是雙射，首先是證明和項，其次是證明歸約步驟和beta歸約。
有多種方式考慮柯里-霍華德對應。在一個方向上，它工作於“把證明編譯為程式”級別上。這裡的“證明”最初被限定為在構造性邏輯中—典型的是直覺邏輯系統中的證明。而“程式”是在常規的函式式編程的意義上的；從語法的觀點上看，這種程式是用某種λ演算表達的。所以柯里-霍華德同構的具體實現是詳細研究如何把來自直覺邏輯的證明寫成λ項。（這是霍華德的貢獻；柯里貢獻了組合子，它是相對於是高級語言的λ演算是能寫所有東西的機器語言）。最近，同樣處理經典邏輯的柯里-霍華德對應的擴展可被公式化了，通過對經典有效規則比如雙重否定除去和皮爾士定律關聯上明確的用續體比如call/cc處理的一類項。
還有一個相反的方向，對一個程式的正確性關聯上“證明提取”的可能性。這在非常豐富的類型論環境中是可行的。實際上理論家對推進非常豐富類型的函式式程式語言的開發的動機，已經部分地混合了希望帶給柯里-霍華德對應更加顯著的地位的因素。
