洛朗定理給出了將一個在圓環域內解析的函式展開成洛朗級數的一般方法,即求出cn代入即可,這種方法為直接法。
基本介紹
- 中文名:洛朗展開式
- 外文名:Laurent expansion
- 適用範圍:數理科學
簡介
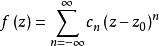

性質
係數計算式
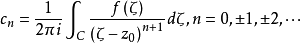
洛朗定理給出了將一個在圓環域內解析的函式展開成洛朗級數的一般方法,即求出cn代入即可,這種方法為直接法。
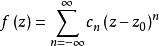

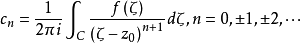
洛朗定理給出了將一個在圓環域內解析的函式展開成洛朗級數的一般方法,即求出cn代入即可,這種方法為直接法。...
洛朗定理定理一 在圓環 內解析的函式f(z)可展成雙邊冪級數 ,其中洛朗定理定理二 若圓環 內的函式f(z)解析,則這個圓環域內的洛朗級數展開式是唯一的。 [1] ...
設C是複平面上的若爾當閉曲線,w=Φ(z)是將C外部映射到{w|Iwl>1}且在∞處規格化的保角映射,那么[Φ(z)]n在∞處有洛朗展開式,稱其中的n次多項式為從...
留數是複變函數中的一個重要概念,指解析函式沿著某一圓環域內包圍某一孤立奇點的任一正向簡單閉曲線的積分值除以2πi。留數數值上等於解析函式的洛朗展開式中負...
設 為 的孤立奇點,在 的去心鄰域 內, 的洛朗級數為:根據展開式的不同情況將孤立奇點分為:(1)可去奇點(2)(m級)極點(3)本性奇點 [1] ...
6 展開式 ▪ 冪級數展開式 ▪ 實用冪級數 7 傅立葉級數 ▪ 三角級數 ▪ 洛朗級數 8 發散性質 9 判別法 ▪ 比較 ▪ 積分 ▪ ...
斯蒂爾吉斯常數,是出現在黎曼ζ函式的羅朗級數展開式中的常數。... 最實用的方法;相反,人們常常通過拼湊已知的泰勒展開式來求出洛朗級數。因為函式的洛朗展開式只要...
第4章解析函式的冪級數展開式4.1解析函式項級數的性質4.2冪級數4.3解析函式的泰勒展開式……習題4第5章解析函式的洛朗展開式5.1解析函式的洛朗級數...
2.5解析函式的泰勒展開式2.6解析函式零點的孤立性及唯一性定理2.7解析函式的洛朗級數展開式2.7.1洛朗級數2.7.2解析函式的洛朗展開式...
第4章解析函式的冪級數展開式4.1解析函式項級數的性質4.2冪級數4.3解析函式的泰勒展開式……習題4第5章解析函式的洛朗展開式5.1解析函式的洛朗級數...
