基本介紹
- 中文名：洛倫茲群
- 外文名：Lorentz group
- 領域：代數
- 性質：典型群
- 相關概念：線性群、酉群、辛群、正交群
- 命名來源：荷蘭物理學家洛倫茨
概念介紹,群,典型群,相關概念,酉群,辛群,正交群,人物簡介,套用領域,
概念介紹
洛倫茨群(Lorentz group)是一類重要的典型群。實數域上使二次型：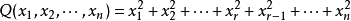
不變的所有n×n實可逆方陣所成的群稱為符號差為(r，n-r)的洛倫茨群。符號差為(3，1)的洛倫茨群在狹義相對論中起著重要的作用。
群
群是一種只有一個運算的、比較簡單的代數結構；是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合，a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”，運算結果稱為“乘積”)滿足：
(1)封閉性，a·b∈G;
(2)結合律，即(a·b)c = a·(b·c);
(3)對G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，則稱G對於所定義的運算“·”構成一個群。例如，所有不等於零的實數，關於通常的乘法構成一個群;時針轉動(關於模12加法)，構成一個群。
滿足交換律的群，稱為交換群。
群是數學最重要的概念之一，已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱，就存在群。例如，可以用研究圖形在變換群下保持不變的性質，來定義各種幾何學，即利用變換群對幾何學進行分類。可以說，不了解群，就不可能理解現代數學。
典型群
典型群是一類重要的群。一般線性群、酉群、辛群、正交群，以及它們的換位子群、對中心的商群等統稱為典型群。實數域和複數域上的典型群是李群的重要例子，它們的構造及表示在李群理論、幾何學、多複變函數論以至物理學中都起著重要作用.迪克森(Dickson，L.E.)通過對有限域上典型群的構造的研究得到了一大批有限單群。這是繼交錯群之後人們發現的又一批重要的有限單群系列.經過謝瓦萊(Chevalley，C.)的工作進一步擴展為有限李型單群的系列後，為有限單群分類的最後完成奠定了一個重要基礎。迪厄多內(Dieudonné，J.)將迪克森的工作加以推廣，通過研究任意體上的典型群的構造也得到了大量的單群。迪厄多內、施賴埃爾(Schreier，O.)、范·德·瓦爾登(Van der Waerden，B.L.)、華羅庚、萬哲先等對研究典型群的構造、自同構及同構作出了重要貢獻。
相關概念
酉群
酉群是一類重要的典型群。在複數域的特殊情形，全體n×n酉方陣在矩陣乘法下構成的群稱為n次酉群，記為U(n)。一般地，設K是帶有對合J：a→a-的體，V是K上n維列向量空間，f(x，y)=x-Hy是V上非退化厄米特型或反厄米特型，這裡H∈GLn(K)且=εH，ε=±1。若A∈GL(V)使f(Ax，Ay)=f(x，y)對所有的x，y∈V成立，則稱A是關於f的酉變換。關於f的全體酉變換組成GL(V)的一個子群，稱為關於f的酉群，記為Un(K，f)。從矩陣的觀點看，Un(K，f)={A∈GLn(K)|HA=H}。當f是交錯雙線性型時Un(K，f)就是辛群Spn(K，f);當K的特徵≠2且f是對稱雙線性型時Un(K，f)就是正交群On(K，f)；當K是複數域，J是復共軛，H=I時，酉群Un(K，f)就是酉群U(n)。
辛群
辛群是一類重要的群。辛空間的自同構群。設(V，ω)是一辛空間，若φ：V→V是線性同構且滿足ω(φX，φY)=ω(X，Y)，X，Y∈V，則稱φ為(V，ω)的一個自同構。(V，ω)的自同構全體構成群GL(V)的一個子群，記為SP(V，ω)。特別地，標準辛空間(K，ω)的自同構群記為Sp(2n，K).若K=R(實數域)，則把Sp(2n，K)簡記為Sp(2n)並稱它為2n維辛群。
正交群
正交群是一類重要的典型群。在實數域的特殊情形，全體n×n正交方陣在矩陣乘法下構成的群稱為n次正交群，記為O(n)。一般地，設V是域K上n維列向量空間，Q(x)=xAx是V上的非退化二次型(A是K上某個n×n矩陣)，若g∈GL(V)使Q(gx)=Q(x)對所有的x∈V成立，則稱g是關於Q的正交變換。關於Q的全體正交變換在映射乘法下構成一個群，稱為關於Q的正交群，記為On(K，Q)。當K的特徵≠2時，V上每個非退化對稱雙線性型f也決定一個正交群。
人物簡介
洛倫茲是荷蘭人，近代卓越的理論物理學家，經典電子論的創立者。因研究磁場對輻射現象的影響而獲1902年諾貝爾物理學獎金。1853年7月18日生於阿納姆，22歲在萊頓大學獲博士學位。他確定了電子在電磁場中所受的力(洛倫茲力)，並預言了正常的塞曼效應。為了解釋邁克耳孫——莫苗實驗的結果，提出了在以太中運動的物體在運動方向上縮短的假說，因而愛爾蘭物理學家菲茨傑拉德同時提出，稱為“洛倫茲-菲茨拉德收縮”，並在以太學說的基礎上提出高速運動的參考錄與靜止參考系之間時間、空間坐標的變換形式，後來稱為“洛倫茲變換”，這些工作與相對論的建立密切有關，他的重要著作是《電子論和它在光現象以及墊輻射中的套用》。1928年2月4日，洛倫茲在荷蘭的哈勒姆逝世，時年74歲。
套用領域
狹義相對論是相對論的一部分。由德國物理學家A·愛因斯坦於1905年提出。基本原理有兩條;(1)狹義相對性原理。即在任何慣性參考系中，自然規律都相同，不存在一種特殊的慣性參考系；或者說，在相對作勻速直線運動的所有慣性系內，一切物理現象的進行都是相同的，描述自然過程的物理學規律不隨參考系而變化；或者還可以換一種說法，在任何慣性系中所作的任何物理實驗，都無法判斷該慣性系是靜止的還是勻速直線運動的。(2)光速不變原理。即在任何慣性系中，真空中的光速C在各個方向都相同，與光源和測光者的運動狀態(速度和方向)都無關;或者說，在所有慣性系內，自由空間中光的速率具有相同的值C。由此得出，時間和空間向量從一個慣性系變換到另一個慣性系時，應滿足洛侖茲變換，而不是滿足伽利略變換。由這一點可導出許多結論：不同地點發生的兩件事是否“同時”，在以恆定速度作相對運動的不同慣性系看來，是不相同的，這就是所謂“同時相對”效應；物體長度的度量是相對的，即運動物體在其運動方向上的長度要比靜止時縮短，這是所謂“動尺縮短”效應；時間的度量也是相對的，即運動的時鐘比靜止的時鐘走得慢，此即所謂“動鐘變慢”；物質的質量是相對的，會隨著物質運動的速度增加而增加，等等。狹義相對論的這些結論，首次從物理學上揭示了時間空間同物質運動的緊密聯繫。但是，這些結論僅適用於慣性系，而真正的、非近似的慣性系實際上並不存在;還有，這些結論乃是觀測效應，對於兩個作相對運動的慣性系來說，都會說對方慣性系中的鐘變慢了、尺縮短了，等等，而不可能承認自己這個慣性系中的鐘變慢了，等等，從而不可能得出雙方公認的結論。把觀測效應的結論，變成有實際意義的結論，是廣義相對論完成的。
