基本介紹
- 中文名:河流地形學
- 外文名:Fluvial geomorphology
- 研究範圍:河流地形發生和發展過程
- 本質:介於陸地水文學和地形學間的科學
- 套用:用於河道治理、地下水開發利用等
- 所屬學科:地理學
研究方法,模擬方法,河流剖面的模擬,斜坡形狀的模擬,水網的模擬,
研究方法
自20世紀50年代以來,地形學的研究方法和手段有了較大進展。
①地形學研究和套用只憑定性描述方法是不夠的,必須用定量方法研究地形過程,說明地形與其形成因素之間的關係。
17、18世紀河流地形研究中曾套用定量方法,但較廣泛的運用是在1945年R.E.霍頓提出了河流長度、數目與級別之間的定量關係之後。較多的是用於地形形態要素的量計,如河流長度、流域面積、地形高度與坡度等,利用這些參數,以數理統計方法開展河流地形特徵、坡地特徵的研究等。由於許多地形過程非常緩慢,一些突發的因素又難以監測,加上影響的因素過於複雜,難以定量地一一表達,因此計量方法在地貌學研究中的運用還很不夠。
⑤地形製圖技術有很大進展,地形圖向定量化、規範化和圖例標準化方向發展。
模擬方法
模擬方法在河流地形學的套用比在地形學其它分支中要先進一些。
河流剖面的模擬
隨機遊動模擬模型可用來模擬河流剖面。剖面上某一點的標高H是相對於河流的基準面測量的。該點被認為是以單位步長移動的,既可以選擇向下移動,也可以選擇向右移動,因此每一步可以有兩種選擇。設其向下移動的機率為p,而在同一水平面上移動的機率為q。由於只有兩種選擇,故p+q=1如果假定河流系統中能量消耗的速率正比於基準面以上的高度(Leopold和Langbein,1962),這個條件可以令向下移步的機率p正比於零點以上的高溫值,而當隨機遊動到達基準面時p為零。機率p和q的逐步變化在模型中可以用圖所示簡單模型中的二個典型的隨機遊動剖面來表示。該模型限制在基準面以上相等增量(0,1,2,3,4,5,)的六個離散高程上。在每一水平面上向下移步的機率為H/6。因此在水平面5向下移步的機率為5/6,而在基底為零。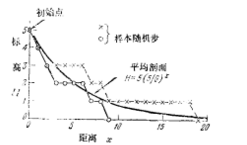 河床的理想指數剖面和兩個隨機遊動模型剖面
河床的理想指數剖面和兩個隨機遊動模型剖面
 河床的理想指數剖面和兩個隨機遊動模型剖面
河床的理想指數剖面和兩個隨機遊動模型剖面在上述的簡單模型中河流長度不受限制的假沒是很不現實的。但建立一個考慮了長度限制的簡單隨機遊動模型還是可能的。例如,模型可以這樣安排,以便在達到給定的距離時或達到給定的距離之前隨機遊動達到基準面。圖說明了兩個理想隨機遊動河流剖面(實線),其中隨機遊動分別限於在6和10個河流---長度單位上。
除河流長度外的另一些限制也可以加到隨機遊動河流模型中。臨時的基準面---如在某一個支流與主流匯合處的標高形成的基準面---可以通過在隨機遊動步長中施加吸收價值來表示。隨機遊動將在最後的吸收堤終止,但臨時基準面的效應可以用一個部分吸收堤來模擬。這種堤可以吸收隨機遊動步長中的給定比例而允許其餘部分毫無影響地通過。
斜坡形狀的模擬
景觀的發育過程可以認為是一個物質從高處向低處運動的運移過程。運移過程既可以作為一個確定性過程來處理,也可以作為一個隨機性過程來處理或者兩者兼有之。例如,一個山脈的“衰變”過程可以認為是一個擴散過程,並可以用基本擴散方程未表示。由方程可得出“衰變”後的地形類似於高斯頻率分布曲線的剖面形狀。擴散方程也可以套用在較小範圍內,如用在Culling(1963)描述的土壤蠕動和局部山坡的發育過程的模型中。
Pollack(1969)通過模擬一段時間內的一系列剖面成功地把經過變形的擴散方程用於模擬深河谷的發育過程。最初他提出三個簡單的模型,其中每一個模型都與在整個河流侵蝕和河谷加寬的綜合過程中地表的下降速度有關。在第一個模型中,整個地表的侵蝕速率是一樣的,並令它等於常數。正如在第二個模型中指出的那樣,我們也可以認為侵蝕的速率正比於標高,高的地區比低的地區侵蝕更快。第二個模型中的常數b可以解釋為是一種對侵蝕的阻抗,它與岩性等因素有關。第三個模型涉及到擴散方程,方程中侵蝕速率與地表的曲率成正比。Pollack將這三個模型中的每一個所描述的某些方面組合成為一個綜合的用下面方程描述的擴散模型
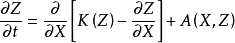
式中Z,X,t分別力標高、距離、時間變數,而K和A描述岩層侵蝕特徵的係數。應當指出,方程本質上是一個帶有與標高有關的擴散係數K(Z)的擴散方程,同時方程中還多加入一項A(X,Z),它代表了河流流動位置的選擇受到空間的限制的那些地方所引起的下切侵蝕速度。在那兒,這個侵蝕速度取決於所在地層河流流動時的阻力。係數K(Z)也與岩層的阻力成正比,它說明了在形成河谷兩壁的斜坡形狀及決定河谷擴寬的速度時所起的作用。
為了對某一特定的侵蝕系統解方程,首先必須用數字形式描述地層剖面的特徵,通常以表格形式列出各地層單位的厚度和特性。
雖然Pollack的模型不是大峽谷剖面的十分的近似,但在考慮了一些純數學簡化後,它的性能是非常符合實際的。它說明建立三維河流侵蝕模型是完全可能的。
水網的模擬
正如已經指出的,河流剖面可以用隨機遊動模型來近似模擬,在模型中隨機遊動的步子是限於要么向下要么在水平向外。從填圖的觀點來看,隨機遊動方法也可以用來模擬水網的發育過程。在這兒限制有點不同。而且在隨機遊動中理所當然的“爬山”步子在這兒應當避免。隨機遊動水網模型已為很多水文工作者和地形學者建立起來。Leopold和Langbein(1962)描述了一個模型,在模型中假定小溪是從坡度均勻的平原上邊發育的,而且開始發育時小溪間的間距相等。在模擬運行開始時,當經過相同的時間增量模型向前推進時,假定小溪總的方向是向下前進的。在每一個時間單位內,描述各個小溪的隨機遊動過程從上一點移動了一個單位距離,規定每一步的運動可以向前也可以向左或向右,但不能向後(上坡)。各種允許方向的運動可以用機率項來考慮。當兩個小溪匯合以後,匯合成的一個單一的小溪又可以用同一規則來處理,以此類推,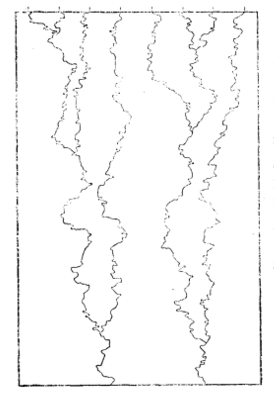 隨機遊動水網的模擬
隨機遊動水網的模擬
 隨機遊動水網的模擬
隨機遊動水網的模擬某一隨機遊動水網模型的結果如圖所示,只是所有規則與上述規則稍有不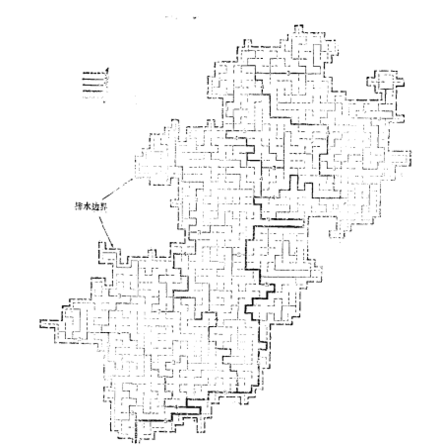 用隨機遊動的方法模擬的排水網
用隨機遊動的方法模擬的排水網
 用隨機遊動的方法模擬的排水網
用隨機遊動的方法模擬的排水網
