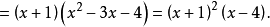求根分解法(factoring method of finding a root)是多項式因式分解的一種方法，指用求多項式的根分離出多項式的一次因式的方法。若多項式f(x)的一個根為x=a，則多項式就含有一次因式x-a，於是f(x)=(x-a)g(x)。例如用綜合除法和餘數定理可求得多項式f(x)=x3+11x2+39x+45的有理二重根為x=-3，有理單根為x=-5，故可將f(x)在有理數域上分解為f(x)=(x+3)2(x+5)。求根分解法常與其他方法結合使用，例如用求根分解法將f(x)在域P上分解為f(x)=(x-a)g(x)後，若g(x)在P上是可約的，則可用其他方法繼續分解g(x)(當然也可仍用求根分解法)，直至將其分解成P上不可約多項式的乘積。求根分解法的關鍵是在指定數集內求多項式的根，利用求根公式是求根的方法之一，對一元二次、三次和四次多項式在複數域和實數域上分解因式時，可直接利用求根公式求多項式的根；但由於五次以上多項式無求根公式，因而可以肯定：在複數域或實數域上不能直接利用求根公式分解五次以上的多項式。
基本介紹
基本介紹,例題解析,
基本介紹
我們知道，多項式f(x)除以x-a的餘數內零，那么,f(x)就能被x-a整除，即x-a就是f(x)的一個因式，反之，亦成立，因此，由餘數定理易得如下著名定理。
因式定理 如果f(a)=0，那么，(x-a)是f(x)的一個因式、反之，如果(x-a)是f(x)的一個因式，那么，f(a)=0，這裡f(a)表x=a時，f(x)的值。
這個定理給出了求多項式的一次因式的一個辦法——求根分解法、即只要a是f(x)的一個根（f(x)的根即指方程f(x)=0的根），則(x-a)就是f(x)的一個因式。如何求f(x)=0的根呢?當f(x)的次數大於2時，求f(x)=0的根也不是一件容易的事(中學教材里只講求一元一次、二次方程的根)，下面介紹一個定理可幫助我們部分解決這個問題。
定理： 如果整係數多項式
這個定理不但為我們找這類方程的根提供了理論依據，而且大大縮小了找根的範圍，例如，要求
的根，我們只需去判定8的約數±1，±2，±4，±8是否是根就行了(不會再有其他有理數根出現),，經試算知，f(±1)=0，f(2)=0，f(-4)=0，所以，f(x)=0有四個根x=±1，2，-4，從而有因式分解：
例題解析
【例1】分解因式
。
法1 ∵4的約數有±1，±2，±4，試算知f(±1)=0，f(4)=0，
∴f(x)有因式(x-1)(x+1)(x-4)(=x3－4x2－x+4)，再用長除法知f(x)÷(x3－4x2－x+4)=(x+1)，故
法2 ∵ f(1)=0，則知 f(x)有因式(x－1)，於是我們可以按此要求(即可提一個公因式(x－1))來拆項、分組,有
由此解法可知，拆項、分組的原則是“求根分解法”.它使拆項、分組方法有了“規律”。
由法1、法2、結合“根”、“長除法”、“綜合除法”、“拆項分組”、可以演変出多種不同的分解形式，這裡就不一一列舉。
在求根時，要特別注意±1是否是根:①如果多項式f(x)中各項係數之和等於零,則1是f(x)的根；②如果f(x)的奇次項係數之和等於偶次項係數之和，則-1是f(x)的根，這兩個結論常用，要記住。
