基本介紹
- 中文名:正交對角拉丁方
- 外文名:orthogonal diagonal Latin squares
- 所屬問題:組合學(組合設計)
- 簡介:一類特殊的正交拉丁方
基本介紹




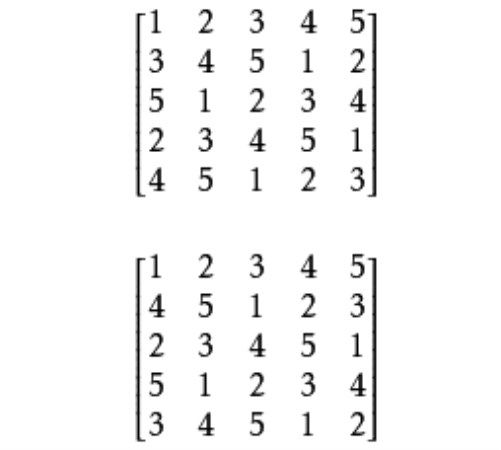




正交對角拉丁方(orthogonal diagonal Latin squares)是一類特殊的正交拉丁方,若一個v階拉丁方的主對角線(位置(i,i),1≤i≤v)與反對角線(位置(i,v+1-i),1≤i≤v)均為截態...
即為一對正交拉丁方。 而在階數固定的情況下,所有兩兩正交的拉丁方所成的集合稱為正交拉丁方族。構造 請你造一個n=4的正交拉丁方陣。如果你有撲克牌,請用四種花色(梅花,方塊,紅心,黑桃)的1(即A)、2、3、4共16張牌,...
正交拉丁方設計是使用正交拉丁方安排的一種試驗方案,當存在m個相互正交的n階拉丁方時,用拉丁方的行和列分別表示兩個因素的n個水平,用這m個拉丁方的記號分別表示其他m個因素的水平,如此包含n2個處理的m十2個因素的試驗方案。概念 ...
正交對稱拉丁方是一類組合對象,與羅姆方等價。值得注意的是正交對稱拉丁方不同於通常的正交拉丁方。若t個n階冪等對稱拉丁方中每兩個構成正交對稱拉丁方,則稱它們是兩兩正交對稱拉丁方。簡介 正交對稱拉丁方是一類組合對象,與羅姆方...
系統研究並解決了區組大小為4,組大小一致且相遇數為2,3,4,6的超單可分組設計的存在性問題;基本解決了區組大小為4,組大小一致且相遇數為2和3的超單可分解可分組設計的存在性問題;解決了強對稱的自正交對角拉丁方的存在性問題...
自正交拉丁方(self-orthogonal Latin square)是一類特殊的拉丁方,指與自身的轉置相正交的拉丁方,亦即(2,1,3)共軛正交拉丁方。v階自正交拉丁方存在的充分必要條件是v≠2,3,6。自正交拉丁方可用來安排一種特殊形式的網球賽,即...
10.5對角正交拉丁方395 10.6素數幻方399 10.6.13階素數幻方400 10.6.24階素數幻方404 10.7積幻方407 10.7.134階積幻方407 10.7.2一類奇數階積幻方408 10.8反幻方409 10.8.13階反幻方410 10.8.2n階反幻方412 10.9...
第2章 拉丁方:數學能做什麼?2.1拉丁方存在嗎?2.2構造任何大小的拉丁方 2.3移位和整除 2.4問題如河水將你帶到遠方 第3章 格列科拉丁方 3.1格列科拉丁方存在嗎?3.2歐拉的格列科拉丁方猜想 3.3互動正交與Gerechte設計 3...
Du Variations》;反證了國際組合數學與套用學會副主席Wallis關於Schroder擬群的猜測; 解決了日本學者Ushio 提出的有關二部圖因子分解的兩個猜想;完成了若干類正交拉丁方型設計,特別是正交對角拉丁方型設計的存在譜的完全刻劃. 主持或...
10.3.2馬步型哈密頓圈421 10.4洛書與幻方424 10.4.1千古洛書425 10.4.2構建n階幻方426 10.5對角正交拉丁方429 10.6素數幻方434 10.6.13階素數幻方434 10.6.24階素數幻方438 10.7積幻方441 10.7.134階積幻方442 ...
設a=k且。k=n,由此得主對角線元全相等的對稱拉丁方.當n為奇數時,共有n個輪,同樣規定c=x且。x=i,由此得冪等對稱拉丁方.除27個可能例外的階數,上述類型的自正交拉丁方及對稱正交侶總是存在的.
