基本介紹
- 中文名:歐拉運動學方程
- 外文名:Eulerkinematicalequations
- 所屬學科:數理科學
- 別名:Euler運動學方程
- 屬性:描述剛體運動的微分方程
- 意義:在剛體繞定點運動研究中很重要
基本介紹
















方程形式



準慣性系中的表達形式




相關概念


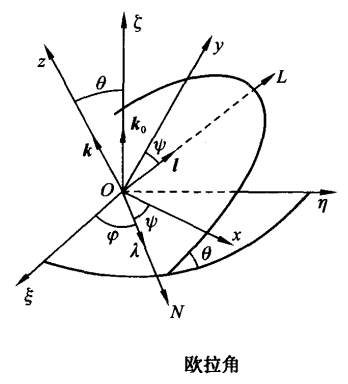


























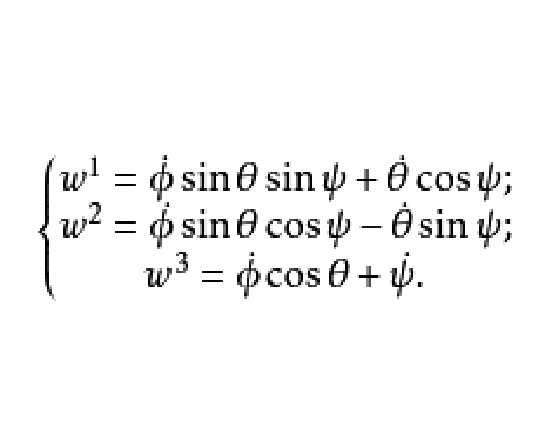




















































適用於航空領域的歐拉運動學方程。其歐拉角定義次序為ZYX。以下是針對於航空次序歐拉角的運動學方程:如圖1所示,紅色的(各軸線較短)坐標系代表地軸系,藍色的(較長)坐標系代表進行一次轉動後的坐標系。第一次繞Z軸旋轉ψ,後依次繞...
因剛體一般運動可由平動和繞質心的轉動合成,故套用質心運動定理和對質心的角動量定理,即可建立剛體一般運動的微分方程。再利用歐拉運動學方程和初始條件,即可確定剛體在空間的一般運動規律。剛體一般運動的研究對研究各種航行器軌跡和姿態...
我們通常把上式叫做歐拉運動學方程。 靜態定義 對於在三維空間裡的一個參考系,任何坐標系的取向,都可以用三個歐拉角來表現。參考系又稱為實驗室參考系,是靜止不動的。而坐標系則固定於剛體,隨著剛體的旋轉而旋轉。參閱右圖2。設定 ...
將歐拉動力學方程同歐拉運動學方程(見歐拉角)結合在一起,就構成求解剛體定點轉動的封閉的運動微分方程組。它是由6個一階非線性微分方程組成;從中消去ω′x、ω′y、ω′Z,可得到對歐拉角θ、ψ、φ的3個二階非線性微分方程。尋...
,向固結與剛體的主軸坐標系投影,即為剛體 定點轉動的動力學方程:上式是歐拉建立的剛體繞定點的運動與所受外力矩之間的關係,稱為歐拉動力學方程。如果以歐拉角ψ,θ,φ描述剛體的方位,則還有歐拉運動學方程:方程(3)與(4)...
3.3.3 歐拉運動學方程 (3.2.7 3.3.1 3.3.2)3.4 剛體的運動方程與平衡方程 3.4.1 力系的簡化 (3.3.2)3.4.2 剛體的平衡問題 (3.3.2 3.4.1)3.5 慣量張量 3.5.1 張量簡介 (3.3.2)3.5.2 剛體的...
1.4 剛體定點運動的幾何方法 1.5 運動學方程和角速度合成定理 1.6 歐拉角及歐拉運動學方程 1.7 卡爾丹角及以卡爾丹表達的運動學方程 1.8 歐拉參數描述的剛體定點運動 1.9 羅德里格參數 1.10 剛體自由運動 1.11 剛體一般...
5.3.4歐拉角、歐拉運動學方程(165)5.4剛體轉動慣量張量(166)5.4.1剛體對任意軸線的轉動慣量(166)5.4.2定點轉動的角動量和動能(168)5.4.3慣量張量(170)5.4.4慣量主軸、主轉動慣量(170)5.5力系的簡化和平衡(173)5.5.1...
第十二章 剛體的定點運動和一般運動 12-1剛體定點運動的實例 12-2位移定理・定點運動剛體的角速度和角加 速度 12-3定點運動剛體內各點的速度和加速度 12-4剛體繞相交軸轉動的合成 12-5歐拉角・歐拉運動學方程 12-6剛體的...
15.平面圖形的運動方程 16.平面運動剛體上各點的速度,瞬時速度中心 17.定瞬心軌跡與動瞬心軌跡 18.平面運動剛體上各點的加速度,瞬時加速度中心 第六章 剛體的定點運動、空間方位定向 19.剛體的定點運動 20.空間方位·歐拉運動學方...
5.3.1 歐拉動力學方程 5.3.2 歐拉運動學方程 5.4 剛體繞定點自由運動 5.4.1 剛體繞定點自由運動的初積分 5.4.2 對稱剛體繞定點自由運動的運動規律 5.5 對稱重剛體的定點運動 5.5.1 對稱重剛體定點運動的初積分 5....
3.1.5剛體的自由運動48 3.2角速度矢量48 3.2.1歐拉角的定義48 3.2.2角速度49 3.2.3剛體定點轉動的速度和加速度50 3.2.4角速度與基點的選擇無關52 3.3剛體定點轉動的基本方程——歐拉運動學方程53 3.4剛體動力學方程55 ...
