基本介紹
- 中文名:剛體定點轉動動力學
- 外文名:dynamics of rotation of a rigid body with a fixed point
剛體定點轉動的動量矩


歐拉動力學方程


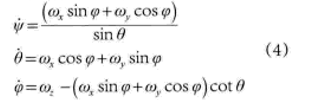

動力學方程的積分









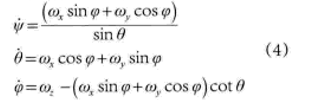






剛體定點轉動動力學(dynamics of rotation of a rigid body with a fixed point) 研究剛體定點轉動時運動與受力關係的學科。剛體動力學的主要組成部分。剛體定點轉動的動量矩...
剛體的定點運動所屬現代詞,指的是剛體上某一點始終保持不動的一種運動。運動原理 如陀螺繞定點O的運動(圖1)。歐拉角 作定點運動的剛體有三個自由度。通常取如下定義的三個歐拉角作為確定剛體位置的獨立參數。建立一個固結在剛體上...
剛體定點轉動動力學 質點動力學以及所有以上論及的剛體動力學分支都有一個共同的特徵:動力學量(動量或需要的動量矩分量)同相應的運動學量(速度或角速度)之間是乘以標量的關係。但是,剛體定點轉動的動力學量——動量矩矢量L同相應的...
定點轉動是指若剛體在運動過程中始終有一個點保持不動(這個點可以是剛體上的,也可以不是剛體上的),這種運動就叫做剛體的定點轉動。剛體作定點轉動時有三個自由度。常用歐拉角作為描寫剛體定點轉動的動力學變數,這時剛體的定點轉動就是...
剛體的運動就象是同剛體固連的本體極錐從空間極錐無滑動地滾過所形成的運動(見剛體定點轉動)。滾動的情況分為外接和內接兩種,分別如圖1和圖2所示。一般情況下的剛體 這種剛體繞固定點的純慣性運動可用分析法或幾何法求解。①分析法...
歐拉動力學方程是剛體動力學的基本方程,剛體定點轉動動力學則是動力學中的經典理論。陀螺力學的形成說明剛體動力學在工程技術中的套用具有重要意義。多剛體系統動力學是20世紀60年代以來由於新技術發展而形成的新分支,其研究方法與經典理論...
第四章 剛體動力學 4.1 剛體的有限轉動 4.2 剛體的無限小轉動 4.3 剛體定點轉動的動力學 4.4 無力矩剛體的定點轉動 4.5 重力場中軸對稱剛體的定點轉動 4.6 剮體的一般運動 習題 第五章 有心力場中的運動 5.1 有心力場...
5.6剛體平面運動動力學(179)5.6.1平面運動的動力學量(179)5.6.2平面運動的微分方程和動能定理(180)5.7圓輪的滾動(185)5.7.1圓輪做無滑動滾動(186)5.7.2圓輪做有滑動滾動(187)5.8 剛體定點轉動動力學(191)5.8.1運動...
第二講:剛體定軸轉動動力學 第一周 剛體(上)測驗 第二周:剛體(下)第一講:以質心為基點處理剛體的平面平行運動 第二講:剛體平面平行運動的瞬時轉軸 第三講:剛體的平衡 第四講:對稱剛體的定點進動現象 本章知識單元和知識點...
2剛體平面運動學和動力學534 目錄第17章剛體的空間運動學549 本章目的549 17.1剛體定點運動549 *17.2矢量相對固定坐標系或平動-轉動 坐標系的導數552 17.3剛體的一般運動557 *17.4平動和轉動參考系下的相對運動 分析566 第18章...
本部分有8章,討論運動穩定性和微擾理論、剛體定點轉動、相對運動動力學、可控力學系統動力學、打擊運動動力學、變質量系統動力學、機電系統動力學、事件空間動力學等內容;第五部分:約束力學系統的積分方法。本部分有6章,介紹降階方法、...
太空飛行器姿態動力學方程是描述太空飛行器在外力矩矩作用下的姿態運動狀態和性質。取參考坐標系(r系)為慣性系,且坐標原點為太空飛行器質心。根據剛體(太空飛行器)定點轉動的角動量定理,則有 式中,H為太空飛行器的角動量;M為作用於太空飛行器的外力矩...
8-3 定軸轉動剛體軸承動反力 靜平衡與動平衡 思考題 習題 第九章 拉格朗日方程 9-1 動力學普遍方程 9-2 拉格朗日方程 9-3 拉格朗日方程的首次積分 9-4 第一類拉格朗日方程 思考題 習題 第十章 剛體動力學(二)10-1 剛體定點...
在進行運動學分析時不考慮系統外物體對其力的作用和剛體相互之間力的作用。建立力與運動的關係是動力學研究的任務。此外,這種關係與物體的慣性有關,故在處理動力學問題時還必須考慮物體的質量分布,這也是動力學與運動學不同之處。簡介...
歐拉運動學方程是描述剛體運動的微分方程,在剛體繞定點運動中,反映角速度和歐拉角關係的方程,該方程在剛體繞定點運動的研究中有重要地位。基本介紹 假定剛體固結參考系 在慣性參考系中有旋轉運動,瞬時旋轉角速度為 ,三個分量記為 ...
剛體在重力作用下,繞旋轉對稱軸上的定點轉動(拉格朗日陀螺)的歐拉動力學方程的解,對三體問題的求解方法有重要貢獻,解決了限制性三體運動的定型問題。拉格朗日對流體運動的理論也有重要貢獻,提出了描述流體運動的拉格朗日方法。方法介紹 拉...
又稱動量矩定理。 質點系對一點(或一軸)的角動量對時間的導數等於外力系對此點(或此軸)的主矩,廣泛用於處理剛體定點(或軸)轉動問題。角動量定理的微分形式為d L /dt= M 。簡介 角動量定理 theory of angular momentum 表述...
早在 18 世紀,歐拉、拉格朗日等許多學者都對高速旋轉剛體作了詳細的研究,並指出這種旋轉的剛體具有進動性和定軸性。尤為突出的是,俄國數學家和物理學家歐拉發表的《剛體繞定點運動理論》這一名著,導出了剛體繞定點轉動的動力學方程,...
剛體運動按運動的特性又可分為:剛體的平動、剛體定軸轉動、剛體平面運動、剛體定點轉動和剛體一般運動。分類 運動學分為質點運動學、剛體運動學和運動約束,為動力學、機械原理(機械學)提供理論基礎,也包含有自然科學和工程技術很多學科...
在研究剛體運動學和剛體動力學中,他得出最基本的結果,其中有:剛體定點有限轉動等價於繞過定點某一軸的轉動,剛體定點運動可用三個角度(稱為歐拉角)的變化來描述;剛體定點轉動時角速度變化和外力矩的關係;定點剛體在不受外力矩時的...
從而式(2)就和轉子無自轉時的單軸轉動微分方程一樣-式(1)可用來確定外力矩M,它等於陀螺力矩 上述近似理論足以解釋高速自轉陀螺儀的全部動力學特性。地球作為一個陀螺,它的姿態攝動也可以由此得到說明(見剛體定點轉動解法)。原理 ...
第1章剛體定點轉動的力學基礎 1.1剛體的角位置與角速度描述方法 1.2常用坐標系 1.3剛體定點轉動的一般原理 第2章加速度的測量與加速度計 2.1加速度測量的力學原理 2.2擺式加速度計 2.3振梁(弦)式加速度計 2.4光纖加速度...
1.3 動量矩、動量矩定理及歐拉動力學方程………14 1.3.1 動量矩及動量矩定理………14 1.3.2 剛體定點轉動的歐拉動力學方程………16 1.4 哥氏加速度、絕對加速度和比力………17 1.4.1 哥氏加速度………17 1.4.2 絕對...
