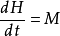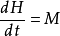基本介紹
發展歷程,研究方法,研究內容,自旋穩定,雙自旋穩定,陀螺體,重力梯度穩定,帶撓性附屬檔案,帶液腔,大型撓性,再入姿態,方程,
發展歷程
太空飛行器姿態動力學是從天體力學關於地球自轉軸運動的歲差和章動理論以及月球繞其質心運動的天平動理論發展起來的。早期的太空飛行器結構比較簡單，在動力學研究中把它當作剛體處理。但是美國“探險者”1 號衛星在飛行中出現了事先沒有預計到的翻滾運動。後來的分析結果表明，問題出在衛星內活動部件的運動。只要放棄理想剛體的假設，代之以準剛體，即內部有能量耗散的近似剛體模型，就能解釋所觀察到的現象。進一步的研究導出了自旋衛星和雙自旋衛星運動穩定性的設計準則。60年代中期對重力梯度穩定衛星可伸展薄壁桿在日光照射下的熱彈性振動的研究，以及對帶撓性天線的自旋衛星穩定性分析表明：撓性振動不僅是姿態控制的干擾，而且是受控對象特性的一部分。70年代初出現的混合坐標法在這方面為控制系統設計和結構設計提供了便利的工具。多剛體系統和剛體液體混合系統動力學也受到重視。到70年代末，以剛體為主體的太空飛行器的姿態動力學問題已基本得到解決。由於太空梭的出現，從70年代後期開始，大型撓性太空飛行器動力學已逐漸成為本學科主要的研究課題。
研究方法
通常是先對太空飛行器及其環境作出簡化假設，建立動力學模型。然後根據力學原理列出描述姿態運動的微分方程，即數學模型。最後用分析方法或計算機仿真來研究運動方程解的性質，從中得出有意義的結論。
常用的太空飛行器模型有剛體、準剛體、彈性體、多剛體、剛體彈性體混合系統、剛體液體混合系統等。作用於太空飛行器的環境力與太空飛行器的軌道有關。人造地球衛星所受的主要環境力是氣動力、重力梯度力、地磁場力矩和太陽輻射壓力矩。它們的數值雖然都很小，但是長時間的作用也會對太空飛行器的姿態運動產生重要影響。另外，氣體噴射、飛輪、天線、太陽電池翼、貯箱內的液體推進劑以及航天員等內部活動物體作用於太空飛行器主體的力矩是內力矩。有的內力矩，如姿態控制噴氣發動機產生的噴射力矩，常被當作外力矩處理。
描述剛體姿態運動的參數常採用歐拉角或歐拉四元素。描述各部分相對運動可以用集中參數或分布參數。運動方程是常微分方程或偏微分方程，視選用的模型而定。運動方程可分為兩類：運動學方程和動力學方程。對於準剛體模型，工程上常用一種近似分析方法──能匯法。它常用於自旋和雙自旋衛星的穩定性分析。對於撓性太空飛行器，運動方程常常是維數很高的常微分方程組或它與偏微分方程的組合。為了進行分析、設計和仿真，必須對運動方程加以簡化。如果太空飛行器各部分間的相對運動很小，而且結構阻尼也很小，則可採用彈性振動理論中的振型坐標法。對於以剛體為主體帶有撓性附屬檔案的太空飛行器模型，可採用以剛體運動參數和振型坐標相結合的方法即混合坐標法來處理。
研究內容
姿態動力學研究下列問題。
自旋穩定
自旋衛星（見人造衛星自旋穩定）的穩定性問題是最早研究的課題之一。如果太空飛行器是理想的剛體，那么它繞最大慣量主軸或最小慣量主軸的自旋運動是穩定的，即小的章動不會增大。若太空飛行器內部存在能量耗散，則只有繞最大慣量主軸的自旋運動才是穩定的，這就是著名的最大軸原理。除穩定性外，研究的課題還有外力矩作用下自旋軸的進動和章動、各種動阻尼方法等。
雙自旋穩定
對雙自旋衛星而言，繞最大慣量主軸的自旋就不一定總是穩定的；而繞最小慣量主軸的自旋也可以是穩定的，只要平台上的能量耗散速率與轉子上的耗散速率之比大於某一數值。這一原理給雙自旋衛星的結構設計帶來靈活性，使它更能適應運載火箭結構尺寸上的限制。有關的研究課題還有平面和轉子能量耗散率估計、章動阻尼方法、自旋軸與慣量主軸不一致時的圓錐擺動、大角度運動和消旋過程的動力學問題。
陀螺體
陀螺體是指安裝有固定軸的高速旋轉的軸對稱轉子的剛體。雙自旋衛星就是一種陀螺體，它的轉子是衛星的主體部分。帶有動量輪的三軸穩定太空飛行器（見太空飛行器三軸姿態控制）也是一種陀螺體，由於動量輪的轉子近似為一剛體，所以這種陀螺體的章動運動總是穩定的。三軸穩定太空飛行器一般採用主動姿態控制。陀螺體有時也有特殊的動力學問題，例如在自旋衛星內一個與衛星自旋軸垂直的轉子加速，能夠使星體消旋並改變衛星的姿態。
重力梯度穩定
衛星上重力桿（見重力梯度穩定）的撓性、熱變形和熱振動也可能引起嚴重的動力學問題。對於重力梯度穩定的陀螺體衛星，內部轉子角動量的大小和方向不同會導致各種不同的可能的平衡狀態。這些平衡狀態的穩定性問題是理論研究的一個課題。
帶撓性附屬檔案
對於帶撓性附屬檔案的三軸穩定太空飛行器，一般用混合坐標法作出簡化模型，供控制系統分析設計用。對於帶有撓性天線的自旋穩定的太空飛行器，用李亞普諾夫方法可證明撓性天線的存在，可能使穩定貯備減小。
帶液腔
對於帶液腔的自旋穩定太空飛行器，內體的液體會降低與能量耗散有關的常規穩定性的貯備。在常規不穩定的條件下還可能引起液體與章動共振，導致更劇烈的動態不穩定。對這類太空飛行器，除穩定性課題外還有對液體耗散能量速率的理論和實驗研究、液體暫存態過程的研究等。對三軸穩定的帶液腔太空飛行器，主要是建立非常微小的體力作用下液體運動的數學模型和研究液體與控制系統的相互作用。
大型撓性
大型撓性太空飛行器不像帶撓性附屬檔案的太空飛行器那樣具有一個剛性的主體，因此它的控制系統頻帶必須覆蓋較多數量的振型，一般採用結構力學方法（如有限元素法）建立數學模型，然後用振型坐標法加以簡化。研究各種模型簡化的準則和方法，以提供具有一定保真度、適合分析設計、數字仿真和太空飛行器上計算等用途的各種數學模型，是這方面動力學的主要課題。
再入姿態
太空飛行器在再入過程中受到的外力是重力和氣動力。再入姿態動力學的基礎是空氣動力學。太空飛行器在再入大氣層時一般要求有穩定的攻角和側滑角。初再入時，實際攻角相對於其平均值（配平攻角）的振盪幅值逐漸減小。隨著高度的下降，攻角振幅可能不斷增加，有時又會重新減小。攻角振盪幅值由姿態控制系統控制。再入時姿態動力學和軌道動力學是密切相關的。有些彈道式再入太空飛行器(見太空飛行器返回技術)在再入過程中繞縱軸自旋，可減小配平攻角所產生的升力對軌道的影響，減小落點散布。具有升力的返回型太空飛行器則設計成有較大的配平攻角,以獲得一定的升力,同時控制繞縱軸的姿態運動，以調節升力在慣性空間的方向，達到調整返回軌道的目的。
方程
太空飛行器姿態動力學方程是描述太空飛行器在外力矩矩作用下的姿態運動狀態和性質。取參考坐標系（r系）為慣性系，且坐標原點為太空飛行器質心。根據剛體（太空飛行器）定點轉動的角動量定理，則有
太空飛行器本體繞某一坐標軸的角動量，不僅取決於此軸的轉速，而且還與其他兩軸的轉速有關。因此，慣量矩陣的選取和調整是太空飛行器任務及總體設計的主要工作內容之一。
