基本介紹
基本信息
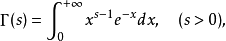
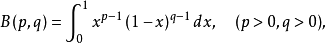

Γ函式
函式表達式

性質

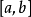



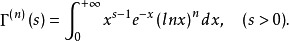

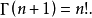



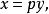
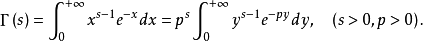
B函式
函式表達式
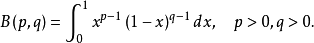
性質
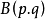
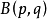


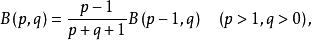


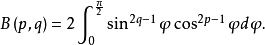
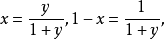

相互關係
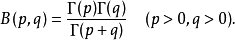
套用


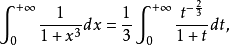



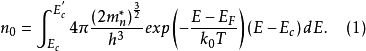



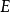
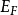
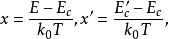



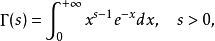
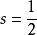
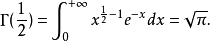


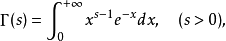
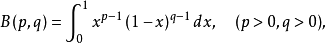



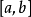



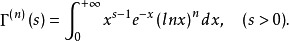

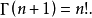



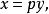
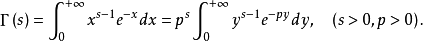
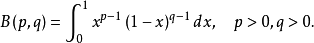
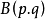
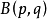


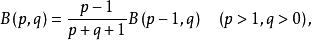


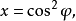
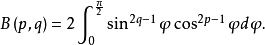
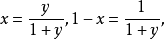

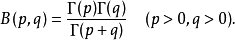


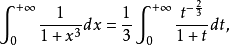



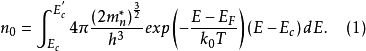



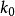
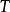
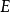
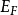
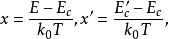



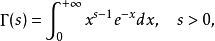
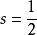
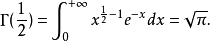


歐拉積分是由瑞士數學家萊昂哈德·歐拉(Leonhard Euler , 1707.4.15~1783.9.18)整理得出的兩類特殊的含參變數的積分。由歐拉積分所定義的函式分別稱為伽馬函式...
《工程數學(1)微積分》是第1冊,內容包括函式與極限、導數與微分、不定積分與定積分、級數、空間解析幾何、偏微分學、重積分、曲線積分、曲面積分理論和廣義積分。...
《工程數學(一)微積分》是2010年由清華大學出版社出版的圖書,作者是王國英。...... 5.3歐拉積分120*第6章微分方程和差分方程簡介1266.1一階微分方程126...
《微積分學習輔導》是2004年科學出版社出版的圖書,作者是陳效群,陳秋桂,顧新身。...... 12.2 含參變數的常義積分12.3 含參變數的廣義積分12.4 歐拉積分...
《微積分和數學分析引論》是科學出版社出版的書籍,作者柯朗、約翰,譯者張鴻林、周民強。本書系統地闡述了微積分學的基本理論。原書分為兩卷,第一卷為單變數函式,...
在機率統計和其他套用學科中會經常用到伽瑪函式和貝塔函式,有的反常積分的計算最後也會歸結為貝塔函式或伽瑪函式。貝塔函式又稱為 B 函式,需要注意這裡 B 是大寫...
Г函式是含參變數的以無窮乘積函式定義的反常積分。作為歐拉積分中一個重要的積分,它與B函式存在一定的聯繫。並且它在定積分也有重要的套用。...
由積分(第一類歐拉積分) 來定義的函式。它與Γ函式的關係:1B(p,q)=Γ(p)Γ(q)/Γ(p+q)也可以由(2)從Γ函式來定義B函式,然後證明(1)式。B函式可用...
7.2 無界函式的廣義積分 7.3 P函式與B函式(歐拉積分) 習題與補充題 第8章 無窮級數 8.1 數項級數及其判斂法則 8.2 函式項級數及其一致收斂性 8.3 冪級數...
他在《歐拉積分計算注釋》(1790)中對歐拉常數進行了較為詳細的計算,得到精確到32位小數的值,被後人稱為歐拉一馬斯凱羅尼常數.在《圓規的幾何學》(1797)中,他從...
劉維爾公式是一個關於多重積分和歐拉積分的公式。...... 劉維爾公式是一個關於多重積分和歐拉積分的公式。中文名 劉維爾公式 外文名 Liouville's Formula 提出...
