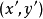次擺線

次擺線

次擺線又稱“長(短)幅旋輪線”，指一個動圓沿著一條定直線作無滑動的滾動時，動圓外或動圓內一定點的軌跡。

基本介紹

  • 中文名：次擺線
  • 外文名：Trochoid
  • 領域：數學
定義,簡介,一般說明,擺線,歷史,方程式,面積,弧長,其它相關聯的曲線,另見,

定義

簡介

次擺線（英語：trochoid），又稱為余擺線、變幅擺線，是指當一個圓沿一條給定直線滾動時，固定在圓所在平面內一定點經過的軌跡。擺線是最常見的一種次擺線。
次擺線的參數方程為：
其中基線所在的為x軸，
為動圓滾過的角度，a為動圓半徑，b為定點與圓心之間的距離。當定點處於圓周上時（b=a）所得到的即為擺線。當定點位於圓外（b>a）或圓內（b<a）時，得到的次擺線又分別稱為長幅擺線（長幅旋輪線）與短幅擺線（短幅旋輪線）。

一般說明

一個一般的方法將一個次擺線定義為一個點的軌跡
圍繞位於的軸線以恆定的速率繞軌道運行
，
或者一個圓形軌道，

擺線

在數學中，擺線（Cycloid）被定義為，一個圓沿一條直線運動時，圓邊界上一定點所形成的軌跡。它是一般旋輪線的一種。
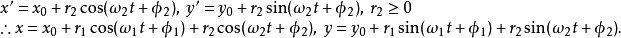
擺線也是最速降線問題和等時降落問題的解。

歷史

擺線的研究最初開始於庫薩的尼古拉，之後馬蘭·梅森也有針對擺線的研究。1599年伽利略為擺線命名。1634年吉勒斯·德·羅貝瓦勒指出擺線下方的面積是生成它的圓面積的三倍。1658年克里斯多佛·雷恩也向人們指出擺線的長度是生成它的圓直徑的四倍。在這一時期，伴隨著許多發現，也出現了眾多有關發現權的爭議，甚至抹殺他人工作的現象，而因此擺線也被人們稱作“幾何學中的海倫”（The Helen of Geometers）。

方程式

過原點半徑為r的擺線參數方程為：
在這裡實參數t是在弧度制下，圓滾動的角度。對每一個給出的t，圓心的坐標為(rt, r)。 通過替換解出t可以求的笛卡爾坐標方程為：
擺線的第一道拱由參數t在(0, 2π)區間內的點組成。
擺線也滿足下面的微分方程：

面積

一條由半徑為r的圓所生成的拱形面積可以由下面的參數方程界定：
微分：
於是可以求得：

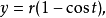
弧長

弧形的長度可以由下面的式子計算出：

其它相關聯的曲線

一些曲線同擺線緊密相關。當我們弱化定點只能固定在圓邊界上時，我們得到了短擺線（curtate cycloid）和長擺線（prolate cycloid），兩者合稱為次擺線（trochoid），前面的情形是定點在圓的內部，後者則是在圓外。次擺線則是上述三種曲線的統稱。更進一步，如果我們讓圓也沿著一個圓滾動而不是直線的話，我們會得到外擺線（epicycloid，沿著圓的外部運動，定點在圓的邊緣），內擺線（hypocycloid，沿著圓內部滾動，定點在圓的邊緣）以及外旋輪線（epitrochoid）和內旋輪線（hypotrochoid，定點可以在圓內的任一點包括邊界。）

另見

相關詞條

熱門詞條

聯絡我們