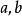橢圓的標準方程共分兩種情況:
當焦點在x軸時,橢圓的標準方程是:x^2/a^2+y^2/b^2=1,(a>b>0);
當焦點在y軸時,橢圓的標準方程是:y^2/a^2+x^2/b^2=1,(a>b>0);
其中a^2-c^2=b^2
推導:PF1+PF2>F1F2(P為橢圓上的點 F為焦點)
基本介紹
- 中文名:橢圓標準方程
- 外文名:Standard equation of the ellipse
- 別稱:線條
- 表達式:x^2/a^2+y^2/b^2=1
- 提出者:數學家
- 提出時間:19世紀
- 套用學科:數學
- 適用領域範圍:數學幾何,解析幾何
- 適用領域範圍:數學,物理
方程推導






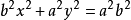
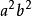

非標準方程
幾何性質
X,Y的範圍
對稱性
計算方法