基本介紹
- 中文名:機率統計計算
- 外文名:The calculation of probability and statistics
- 又稱:計算機率統計
- 性質:箭頭指示出可選用的統計模型
- 學科:機率論、數理統計
概念
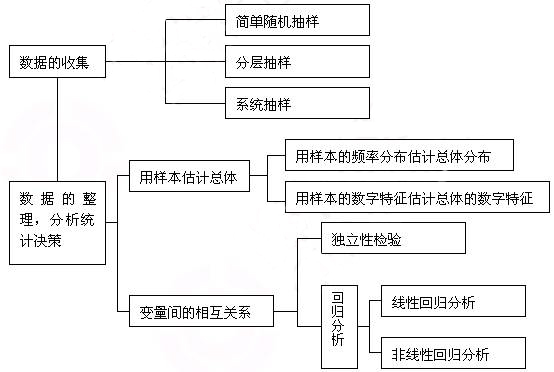



機率統計計算,又稱計算機率統計,是機率論、數理統計、計算數學和計算機科學等學科之間的一個交叉性、邊緣性、套用性的學科分支。...
機率統計是研究自然界中隨機現象統計規律的數學方法,叫做機率統計,又稱數理統計方法。機率統計主要研究對象為隨機事件、隨機變數以及隨機過程。機率統計是套用機率的理論...
《計算統計》是2009年09月人民郵電出版社出版的一本圖書,作者是(美國)吉文斯。本書主要介紹了經典的統計計算方法,並通過實例對這些方法的套用進行了較詳細的說明。...
許多統計分析方法都是以常態分配為基礎的。此外,還有不少隨機變數的機率分布在...關於常態分配的機率計算,我們先從標準常態分配著手。這是因為,一方面標準正態...
條件機率:已知事件B出現的條件下A出現的機率,稱為條件機率,記作:P(A|B)...圖集 機率計算圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:20次歷史版本...
機率統計定義 在一定條件下,重複做n次試驗,nA為n次試驗中事件A發生的次數,...“均勻分布”性,事件A發生的機率取為:P(A)=μ(A)/μ(S),這樣計算的機率...
全書共分為8章:第1章為事件及其機率的概念與計算;第2,3章為隨機及其分布;第4章為隨機變數的數字特徵;第5章為極限定理;第6章為數理統計的基本概念;第7,8章...
《機率論與數理統計》是中國質檢出版社出版的一本圖書,有陳愛江和張文良主編。《機率統計》是高等院校理工類、經管類的重要課程之一。在考研數學中的比重大約占22%...
需要提及的是下面將要介紹的9個計算機率的定理與上面已經提及的事件的計算沒有關係,所有關於機率的定理均由機率的3個公理得來,同時適用於包括拉普拉斯機率和統計機率...
《機率論和數理統計》是高等院校理工類、經管類的重要課程之一。在考研數學中的比重大約占22%左右。主要內容包括:機率論的基本概念、隨機變數及其機率分布、數字特徵...
《統計計算》是北京大學出版社於1995-7出版的書籍,作者高惠璇...... 《統計計算》可作為理工科院校機率統計、數學、套用數學、計算機科學等系大學生的教材,也可作為...
它是根據原資料作出一個總體指標是否等於某一個數值,某一隨機變數是否服從某種機率分布的假設,然後利用樣本資料採用一定的統計方法計算出有關檢驗的統計量,依據一定的...
統計計算與模擬(Journal of Statistical Computationand Simulation) Taylor & Francis公司的期刊。月刊。創刊於1972年。發表統計領域相關的文章,包括與機率論和統計相關...
《機率論與統計學(經濟管理類)》主要是為經濟、管理專業大學生編寫的教材。全書七章,前三章講機率,是為學習統計學作準備的。後四章是《機率論與統計學》重點,...
《機率統計(第4版)》是2014年清華大學出版社出版的圖書,作者是隋亞莉、曲子芳。...... 全書共分為8章:第1章為事件及其機率的概念與計算;第2,3章為隨機變數及...
《機率與統計》是2009年華中科技大學出版社出版的圖書,作者是龔友運、李學銀。本書介紹了機率論的基本知識和常用的數理統計方法。...
《機率統計》是2012年7月機械工業出版社出版的圖書,作者是美國作家Morris H.DeGroot、Mark J.Schervish。...
《機率論與數理統計》是2016年清華大學出版社出版的圖書,作者是王信峰、李承耕。...... 機率論與數理統計內容簡介 編輯 本書共八章:第1章,隨機事件及機率計算;...
機率除法公式即一事件關於 另一事件的條件機率的計算公式。 ...... 機率除法公式即一事件關於 另一事件的條件機率的計算公式。 [1] 參考資料 1. 鄭家亨,統計大...
方差的概念與計算公式,例如 兩人的5次測驗成績如下:X: 50,100,100,60,50,...中公考研 考研數學 機率論與數理統計專項輔導[M]. 2017 3. 王橋. 方差的幾...
這個免費的數學應用程式的各種功能的計算器是一個統計:- 統計:您是能夠計算出...如果你是一個學生,這將有助於您了解統計和機率理論。注:統計數據收集,整理,...
機率依其計算方法不同,可分為古典機率、試驗機率和主觀機率[1]。在許多實際問題中,要將全部觀察或試驗結果列舉出來往往是不可能的,同時,試驗結果的等可能性假定...
大數定律(law of large numbers),是一種描述當試驗次數很大時所呈現的機率性質...例如,沒有學過微積分的學生也可以輕鬆利用excel或計算器計算樣本均值等統計量,...
