基本介紹
- 中文名:機率乘法定理
- 外文名:multiplication theorem of probability


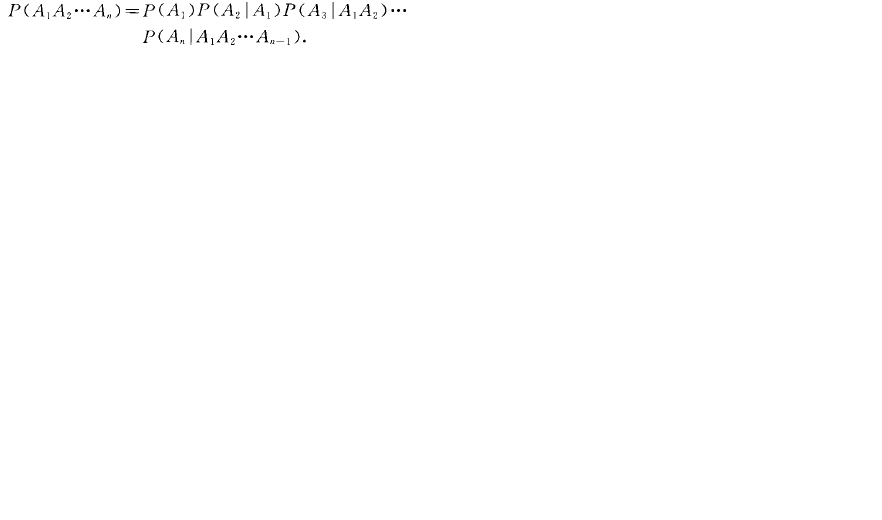
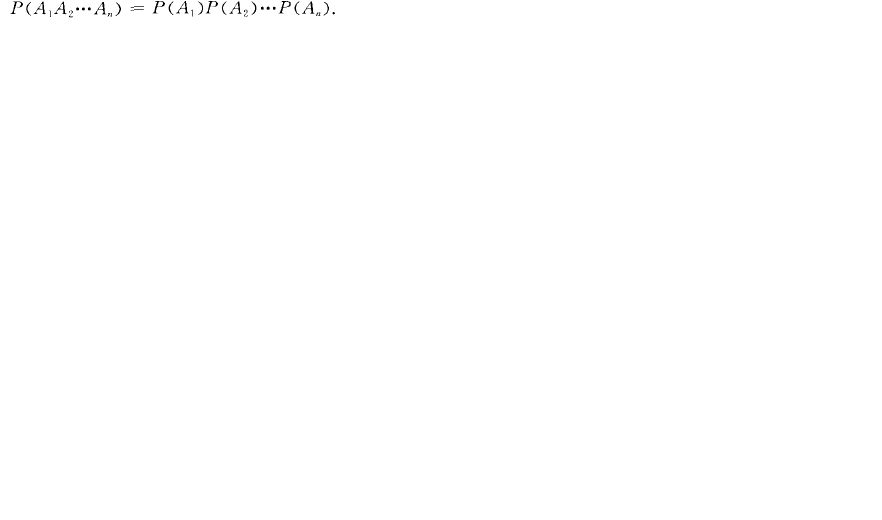



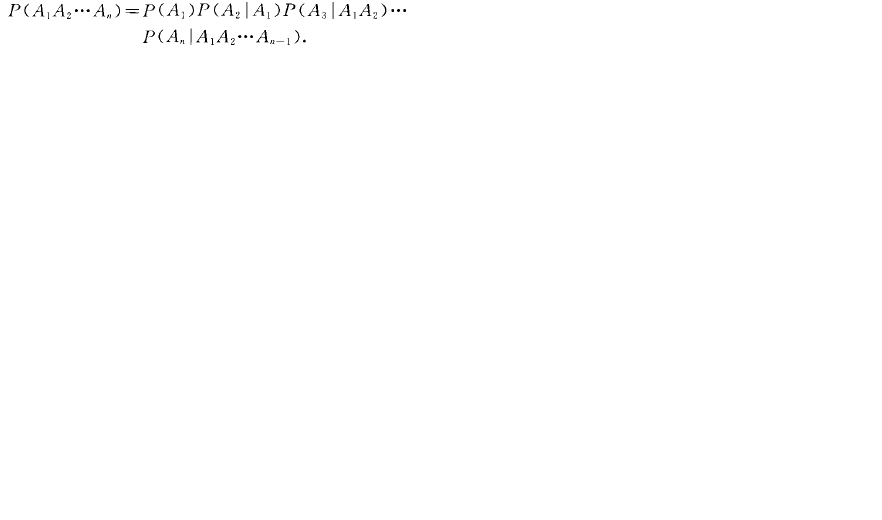
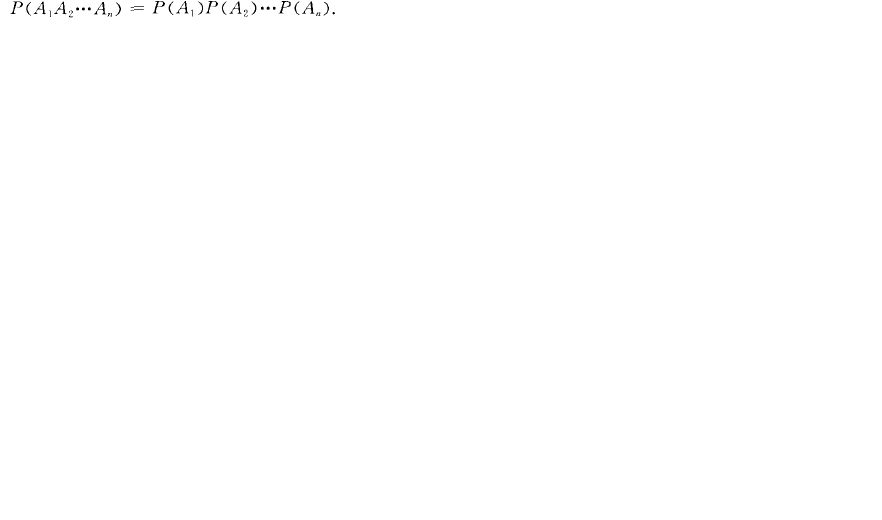
所以,一個孩子表現的正常機率是:1/4(AA)+1/4(Aa)+1/4(Aa)=3/4 說明:括弧內的內容是說明前面的1/4,不是相乘的關係。這就是遺傳學中的加法定理。階乘公式:n! (如9的階乘就是9!)在百度里輸入“9!”的組合就知道...
2.4 機率的性質 2.5 機率的基本運算法則 2.5.1 機率的乘法定理 2.5.2 全機率公式 2.5.3.Bayes定理 2.5.4 貝葉斯(Bayes)推斷簡介 2.5.5 獨立性 2.6 獨立重複試驗模型(或伯努利概型)第3章 隨機變數及其分布 3.1.一元...
第一節 條件機率乘法定理 第二節 全機率公式 第三節 貝葉斯(Bayes)公式 第四節 事件的相互獨立性 第五節 重複獨立試驗 二項機率公式 習題四 第五章 一維隨機變數 第一節 一維隨機變數及其分布函式 第二節 離散型隨機變數 第三...
1.3 機率的加法定理 1.4 條件機率與乘法定理 1.5 獨立實驗概型 1.6 典型例題分析 習題一 本章小結 第2章 隨機變數及其分布 2.1 離散型隨機變數 2.2 分布函式 2.3 連續型隨機變數 2.4 常態分配 2.5 隨機變數函式的分布...
2.1 條件機率、乘法定理 22 2.2 全機率公式 25 2.3 貝葉斯公式 26 2.4 事件的獨立性 27 2.5 重複獨立試驗、二項機率公式 32 習題2 37 第3章 隨機變數及其分布 40 3 1 隨機變數的概念 40 3.2 離散型隨機變數 41 3.3...
2020年7月20日,《機率論與數理統計(第三版)》由高等教育出版社出版發行。內容簡介 該書內容包括隨機事件與機率、條件機率與獨立性、隨機變數及其分布、多維隨機變數及其分布、隨機變數的數字特徵與極限定理、數理統計的基本概念、參數...
第一章 隨機事件與機率 §1.1隨機試驗與樣本空間 §1.2隨機事件及其機率 一、隨機事件 二、事件間的關係與運算 三、頻率與機率 §1.3古典概型 §1.4機率的基本性質 §1.5條件機率與事件的獨立性 一、條件機率 二、乘法定理 ...
4 隨機事件與機率 4.1 隨機事件 4.2 機率與計算 4.3 條件機率與乘法定理 4.4 *全機率公式與貝葉斯公式 習題四 5 隨機變數及其數字特徵 5.1 隨機變數及其分布函式 5.2 隨機變數的數字特徵 5.3 幾種常用機率分布 習題五 ...
一、條件機率與乘法定理 二、全機率公式與Baves公式 第四節 事件的獨立性 一、事件的獨立性 二、伯努利概型 第五節 套用實例 一、生日問題 二、贈送問題 習題 第二章 隨機變數及其分布 第一節 隨機變數的概念 第二節 一維離散型...
2.1 條件機率. 乘法定理 2.2 全機率公式 2.3 貝葉斯公式 2.4 事件的獨立性 2.5 重複獨立試驗. 二項機率公式 習題二 第三章 隨機變數及其分布 3.1 隨機變數的概念 3.2 離散型隨機變數 3.3 隨機變數的分布函式 3.4 連續...
1.2頻率和機率 1.2.1頻率 1.2.2機率 1.3古典概型 1.4條件機率、全機率公式和貝葉斯公式 1.4.1條件機率 1.4.2乘法定理 1.4.3全機率公式和貝葉斯公式 1.5事件的獨立性 1.6伯努利概型 本章小結 習題1 第2章隨機變數...
第一章 機率與隨機變數 1 1.1 機率的基本概念 1 1.2 機率的基本定理 3 1.2.1 機率加法定理 4 1.2.2 機率乘法定理 5 1.2.3 全機率公式 6 1.2.4 假設機率公式 7 1.3 隨機變數及其分布 8 1.3.1 離散隨機...
乘積極限法 乘積極限法,即kaplan-meier法。適用範圍:小樣本未分組資料、大樣本未分組資料,可利用機率乘法定理來計算生存率。
1)最大似然法:用於自變數均為分類變數的情況,該方法建立在獨立事件機率乘法定理的基礎上,根據訓練樣品信息求得自變數各種組合情況下樣品被封為任何一類的機率。當新樣品進入是,則計算它被分到每一類中去的條件機率(似然值),機率最...
