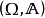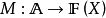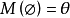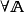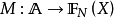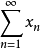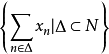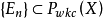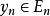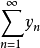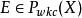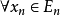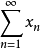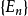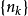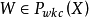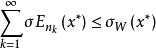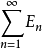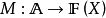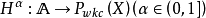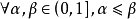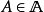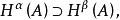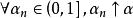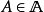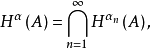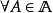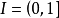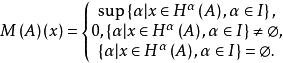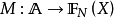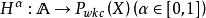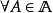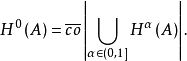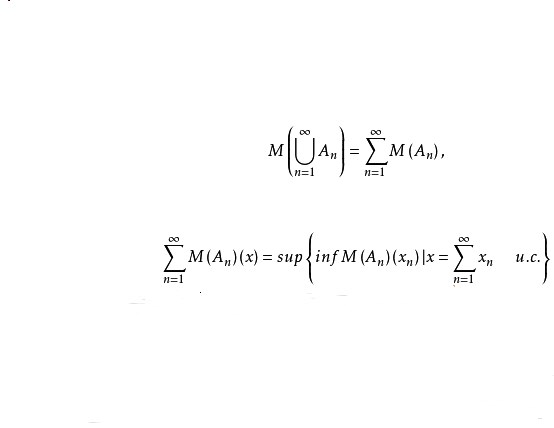模糊數測度

模糊數測度(measures taking fuzzy number)也稱模糊集值測度，是一類集值測度的推廣，它是取值為m維歐氏空間R^m上的模糊數的一種可加集函式。模糊數測度是張文修於1986年引進的，現已廣泛套用於經濟系統理論研究中。隨機模糊數的不定積分是模糊數測度。

基本介紹

• 中文名：模糊數測度
• 外文名：measures taking fuzzy number
• 所屬學科：數學(模糊數學)
• 別稱：模糊集值測度
• 簡介：一類集值測度的推廣
• 提出者：張文修

發展過程

模糊集值測度(即模糊數測度)與模糊集值積分(模糊數積分)是集值測度與集值積分的推廣，首先我們回顧集值測度與積分的發展概況。集值測度與積分是伴隨著本世紀40年代集值映射的提出和發展而產生的。1965年，Aumann在經濟學問題的啟發下，以可測集值映射的單值Lebesgue可積選擇定義了Rⁿ空間中集值映射的積分，稱為Aumann積分。其他一些學者成功地將該積分理論運用於最優控制系統。1970年，Datko首先將Aumann等人在Rⁿ中的結果推廣到了Banach空間，開始了Banach空間集值映射積分理論的研究。Hiai給出了可積有界集值映射的積分表示，並討論了集值條件期望和鞅的存在性。進入80年代以後，Papageorgiou的工作具有代表性，他在十分廣泛的意義下，建立了集值映射的Fatou引理，以及弱收斂意義下的積分收斂定理和集值映射弱收斂與其支撐弱收斂的等價關係。薛小平以Pettis積分為工具，在Banach空間上建立了集值函式弱意義下的積分，即Pettis-Aumann積分，找到了集值函式可表成Pettis-Aumann積分的條件。

集值映射積分理論的發展，促進了集值測度的產生和發展。1972年，Artstein率先在Rⁿ空間中引入集值測度的概念，得到了一些重要結果。其後，1978年，Hiai對取值於Banach空間的集值測度進行了討論，對有界變差的集值測度以空間的幾何性質為工具建立了Artstein的相應結果。Papageorgiou進一步推廣和補充了Hiai的工作。特別地，他給出了測度變換的表示定理。張文修等人利用Artstein的選擇定理討論了由單值測度生成集值測度的條件，薛小平利用不依賴於有限維特點的方法，將上述有界閉凸值集值測度的表示定理推廣到可分自反實Banach空間的情形，且給出了生成集值測度為有界變差的條件，集值測度與集值積分作為60年代後期發展起來的一門新興理論，它的產生和發展始終伴隨著在經濟學、控制論、最最佳化、非光滑分析以及統計學等眾多領域的套用。

自從模糊數的概念出現以後，人們自然地考慮基於模糊數的測度與積分問題。因此，有關集值映射的可測性、可積性和可微性等概念也先後推廣到模糊集值映射的情形。1986年，Puri和Rales-cu在Rⁿ上給出了模糊隨機變數及模糊隨機變數的期望的概念，它們分別是Rⁿ上隨機變數(集值映射)及Aumann積分的自然推廣。1982年，張文修幅在Rⁿ中定義r¨一種模糊數測度(模糊集值測度)，給出了模糊數測度與集值測度的關係及模糊數測度的lebesgue分解。此外，關於模糊集值映射(模糊數)的級數、序列、廣義積分以及不動點等問題，也得到了一定程度的進展。由於空間結構的複雜性，對集值測度與積分的討論遠比經典測度與積分困難得多，從而對做為集值測度與積分推廣的模糊集值測度與積分的討論自然也是困難的。

模糊數測度的定義

定義1 設是一個可測空間，稱為一個廣義模糊數測度，如果M滿足下述條件

1) ；

2) 的不交集列，有

此處定義為

又若滿足上述條件1)，2)，則稱M為正規模糊數測度。

模糊數測度與集值測度的關係

引理1 設N表示自然數集，如果級數在X中是無條件收斂的，則集是X中相對弱緊集。

引理2 設，且存在，級數無條件收斂，如果存在一個使得，則，級數無條件收斂。

注 可得下述結論：設是一個一致有界集列，如果任意自然數的子序列，均存在一個，使得，則無條件收斂。

有了上述引理，我們可得如下結論．

定理1 映射是一個廣義模糊數測度若且唯若存在一族集值測度滿足下述條件

1)且，有

2)且，有。

3)，令則有

定理2 映射是一個正規模糊數測度若且唯若存在一族集值測度滿足上述定理1的條件1)-3)外，還滿足下述條件：

4)，有